��Ŀ����
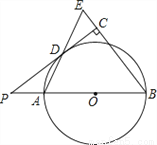
��ͼ����֪AB�ǡ�O��ֱ������P��BA���ӳ����ϣ�PD�С�O�ڵ�D������B��BE��ֱ��PD����PD���ӳ����ڵ�C������AD���ӳ�����BE�ڵ�E��
��1����֤��AB=BE��
��2����PA=2��cosB=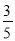 �����O�뾶�ij���
�����O�뾶�ij���
��ϰ��ϵ�д�
 ������������ϵ�д�
������������ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����֪AB�ǡ�O��ֱ������P��BA���ӳ����ϣ�PD�С�O�ڵ�D������B��BE��ֱ��PD����PD���ӳ����ڵ�C������AD���ӳ�����BE�ڵ�E��
��1����֤��AB=BE��
��2����PA=2��cosB=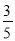 �����O�뾶�ij���
�����O�뾶�ij���

 ������������ϵ�д�
������������ϵ�д�