题目内容
2.如果a+b≤a-b,那么( )| A. | b<0 | B. | b≤0 | C. | a>0 | D. | 无法确定b的取值 |
分析 由不等式的基本性质1和基本性质2得出b≤0即可.
解答 解:∵a+b≤a-b,
∴2b≤0,
∴b≤0;
故选:B.
点评 本题考查了不等式的基本性质;熟练掌握不等式的基本性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在平面直角坐标系中,以点O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,则这个平行四边形的第四个顶点坐标不可能是( )
| A. | (2,-1) | B. | (-2,1) | C. | (-3,1) | D. | (4,1) |
13.若x1、x2是方程2x2-3x-4=0的两根,则x1x2=( )
| A. | 0 | B. | 2 | C. | -2 | D. | -4 |
14.用较小的数减去较大的数,其结果一定为( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 无法确定 |
11.下列计算错误的是( )
| A. | $\frac{b}{a-b}$-$\frac{a}{a-b}$=-1 | B. | $\frac{x-3y}{a+b}$-$\frac{x-2y}{a+b}$=-$\frac{y}{a+b}$ | ||
| C. | 1÷$\frac{b}{a}$×$\frac{a}{b}$=1 | D. | $\frac{1}{(a+b)^{2}}$•$\frac{{a}^{2}-{b}^{2}}{a-b}$=$\frac{1}{a+b}$ |
12.若关于x的一元一次方程k(x+4)-2k-x=5的解为x=-3,则k的值是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
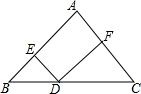 如图,已知点D在△ABC边BC上,且与B,D不重合,AC∥DE,AB∥DF,BC=5.
如图,已知点D在△ABC边BC上,且与B,D不重合,AC∥DE,AB∥DF,BC=5.