题目内容
16.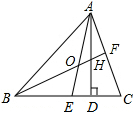 如图,在△ABC中,AD是高线,AE、BF是角平分线,已知∠C=70°.
如图,在△ABC中,AD是高线,AE、BF是角平分线,已知∠C=70°.(1)求∠BOA的度数.
(2)若∠BAC=50°,求∠AFB,∠DAE的度数.
分析 (1)根据三角形内角和定理求出∠CAB+∠CBA,根据角平分线的定义求出∠OAB+∠OBA,根据三角形内角和定理计算即可;
(2)根据角平分线的定义、三角形内角和定理计算即可.
解答 解:(1)∵∠C=70°,
∴∠CAB+∠CBA=110°,
∵AE、BF是角平分线,
∴∠OAB+∠OBA=$\frac{1}{2}$×(∠CAB+∠CBA)=55°,
∴∠BOA=180°-(∠OAB+∠OBA)=125°;
(2)∵∠C=70°,∠BAC=50°,
∴∠ABC=180°-70°-50°=60°,
∵BF平分∠ABC,
∴FBC=$\frac{1}{2}$∠ABC=30°,
∴∠AFB=∠FBC+∠C=100°,
∵AE平分∠BAC,
∴∠EAC=$\frac{1}{2}$∠BAC=25°,
∵AD是高线,∠C=70°,
∴∠CAD=20°,
∴∠DAE=∠EAC-∠DAC=5°.
点评 本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
6.下列各式中运算正确的是( )
| A. | 6a-5a=1 | B. | a2+a2=a4 | C. | 3ab-4ba=-ab | D. | a+2a2=3a3 |
4.把抛物线y=-(x+1)2-2绕原点旋转180°后,得到的抛物线为( )
| A. | y=(x+1)2-2 | B. | y=(x-1)2-2 | C. | y=(x-1)2+2 | D. | y=(x+1)2-2 |
1.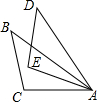 如图,下列条件中,不能证明△ABC≌△ADE的是( )
如图,下列条件中,不能证明△ABC≌△ADE的是( )
 如图,下列条件中,不能证明△ABC≌△ADE的是( )
如图,下列条件中,不能证明△ABC≌△ADE的是( )| A. | ∠B=∠D,∠C=∠E,AC=AE | B. | AB=AD,∠B=∠D,BC=DE | ||
| C. | AC=AE,AB=AD,∠B=∠D | D. | AC=AE,BC=DE,AB=AD |
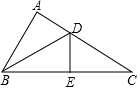 如图,在△ABC中,∠A=90°,BC的垂直平分线交BC于E,交AC于D,且AD=DE
如图,在△ABC中,∠A=90°,BC的垂直平分线交BC于E,交AC于D,且AD=DE