题目内容
4．把抛物线y=-（x+1）2-2绕原点旋转180°后，得到的抛物线为（ ）| A． | y=（x+1）2-2 | B． | y=（x-1）2-2 | C． | y=（x-1）2+2 | D． | y=（x+1）2-2 |
分析 当抛物线y=-（x+1）2-2绕原点旋转180°后抛物线的顶点坐标为（1，2），并且开口方向相反，于是根据顶点式写出旋转后的抛物线解析式．
解答 解：由于抛物线y=-（x+1）2-2绕原点旋转180°后抛物线的顶点坐标为（1，2），并且开口方向相反，则所得抛物线解析式为y=（x-1）2+2．
故选：C．
点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
阅读快车系列答案
相关题目
14．下列说法正确的是（ ）
| A． | -$\sqrt{5}$的相反数是$\sqrt{5}$ | B． | 负数没有立方根 | C． | 1平方根是1 | D． | 0没有平方根 |
15．
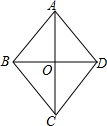如图，在菱形ABCD中，AC与BD相交于点O，AO=4，BO=3，则菱形的边长AB等于（ ）
如图，在菱形ABCD中，AC与BD相交于点O，AO=4，BO=3，则菱形的边长AB等于（ ）| A． | 10 | B． | $\sqrt{7}$ | C． | 6 | D． | 5 |
12．以下列各组线段为边，能组成三角形的是（ ）
| A． | 1，2，3 | B． | 3，3，6 | C． | 5，8，2 | D． | 4，5，6 |
9．计算6m2-5m+3与5m2+2m-1的差，结果是（ ）
| A． | m2-3m+4 | B． | m2-3m+2 | C． | m2-7m+2 | D． | m2-7m+4 |
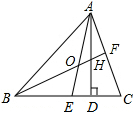如图，在△ABC中，AD是高线，AE、BF是角平分线，已知∠C=70°．
如图，有长为24m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆的矩形花圃．