题目内容
4．一组按规律排列的式子：$\frac{2}{a}$，$\frac{4}{a^3}$，$\frac{6}{a^5}$，$\frac{8}{a^7}$，…．则第n个式子是$\frac{{2}^{n}}{{a}^{2n-1}}$．分析 观察分子、分母的变化规律，总结出一般规律即可．
解答 解：2，4，6，8…，分子可表示为：2n，
1，3，5，7，…分母可表示为a2n-1，
则第n个式子为：$\frac{{2}^{n}}{{a}^{2n-1}}$．
故答案是：$\frac{{2}^{n}}{{a}^{2n-1}}$．
点评 本题考查了单项式的知识，属于基础题，关键是观察分子、分母的变化规律．
练习册系列答案
名校课堂系列答案
相关题目
有10个边长为1的正方形，排列形式如下左图．请在左图中把它们分割，使之拼接成一个大正方形，并把分割后的图形画在右图的正方形网格中．（正方形网格中的每个小正方形边长都是1，每个小格顶点为格点，要求以格点为顶点画大正方形）
12．在式子：2x-y=3中，把它改写成用含x的代数式表示y，正确的是（ ）
| A． | y=2x+3 | B． | y=2x-3 | C． | x=$\frac{3-y}{2}$ | D． | x=$\frac{3+y}{2}$ |
清明小长假的第二天上午8时，小张自驾小汽车从家出发，带全家人去离家200千米的一个4A级景区游玩，小张驾驶的小汽车离家的距离y（千米）与时间t（时）之间的关系如图所示，请结合图象解决下列问题：
如图，三角形DEF是三角形ABC经过某种变换得到的图形，点A与点D，点B与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：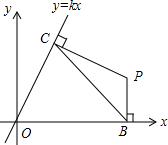
如图，在平面直角坐标系中，直线y=kx（k≠0）经过点（a，$\sqrt{3}$a）（a＞0），线段BC的两个端点分别在x轴与直线y=kx上（点B、C均与原点O不重合）滑动，且BC=2，分别作BP⊥x轴，CP⊥直线y=kx，交点为P．经探究，在整个滑动过程中，P、O两点间的距离为定值$\frac{4}{3}\sqrt{3}$．
已知一长方形的长为8，宽为4，请建立恰当的平面直角坐标系，并求出A、B、C、D四点坐标．