题目内容
已知a=
+
,b=
,则a与b的大小关系是a b.
| 5 |
| 6 |
| 1 | ||||
|
考点:分母有理化
专题:
分析:将b=
进行分母有理化,再与a比较即可.
| 1 | ||||
|
解答:解:∵b=
=
=
+
,
又a=
+
,
∴a=b.
故答案为:=.
| 1 | ||||
|
| ||||||||
(
|
| 6 |
| 5 |
又a=
| 5 |
| 6 |
∴a=b.
故答案为:=.
点评:本题考查了分母有理化:两个含二次根式的代数式相乘时,它们的积不含二次根式,这样的两个代数式成互为有理化因式.二次根式的分母有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
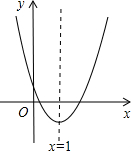 已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=1.下列结论:①abc>O,②2a+b=O,③b2-4ac<O,④x=2与x=0时的函数值相等.其中正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=1.下列结论:①abc>O,②2a+b=O,③b2-4ac<O,④x=2与x=0时的函数值相等.其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
点A在数轴上距原点5个单位长度,将A点先向左移动2个单位长度,再向右移动6个单位长度,此时A点所表示的数是( )
| A、-1 | B、9 |
| C、-1或9 | D、1或9 |
计算
÷
•(a2-b2)的结果是( )
| 1 |
| 2 |
| a-b |
| 2a+2b |
A、
| ||
B、
| ||
C、
| ||
| D、(a+b)2 |