题目内容
已知（x-1）（x+3）（x-4）（x-8）+k是完全平方式，试求k的值．
考点：完全平方式
专题：
分析：先根据多项式的乘法分别计算（x-1）（x-4）与（x-8）（x+3），再化简得出（x2-5x）2-2×10×（x2-5x）-96+k，因为（x2-5x）2-2×10×（x2-5x）-96+k是个完全平方式，所以k-96=102，即可得k的值．
解答：解：（x-1）（x+3）（x-4）（x-8）+k
=[（x-1）（x-4）][（x-8）（x+3）]+k
=（x2-5x+4）（x2-5x-24）+k
=（x2-5x）2-20（x2-5x）-96+k
=（x2-5x）2-2×10×（x2-5x）-96+k
因为（x2-5x）2-2×10×（x2-5x）-96+k是个完全平方式，所以
k-96=102
k=196．
=[（x-1）（x-4）][（x-8）（x+3）]+k
=（x2-5x+4）（x2-5x-24）+k
=（x2-5x）2-20（x2-5x）-96+k
=（x2-5x）2-2×10×（x2-5x）-96+k
因为（x2-5x）2-2×10×（x2-5x）-96+k是个完全平方式，所以
k-96=102
k=196．
点评：本题考查了完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．
练习册系列答案
阅读快车系列答案
相关题目
如图在△ABC中，∠B=30°，AD⊥AB，垂足为A，AD=1cm，求AB的长．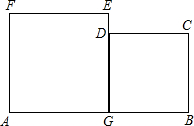
如图所示，这是一块工厂的下脚料铁板，其中AGEF和BCDG都是正方形．某个体水箱加工生产户经过计算得知，这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积（切割，焊接过程中的面积不变），他思考了一会，决定购买这块下脚料用于焊接冰箱．请你利用所学的知识帮助他设计一种最简便的切割，焊接方法，并证明你的设计方案．
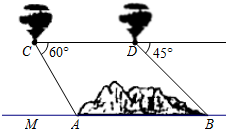如图，我省在修建泛亚铁路时遇到一座山，要从A地向B地修一条隧道（A，B在同一水平面上），为了测量A，B两地之间的距离，某工程师乘坐热气球从M地出发垂直上升150 米到达C处，在C处观察A地的俯角为60°，然后保持同一高度向前平移200米到达D处，在D处观察B地的俯角为45°，则A、B两地之间的距离为多少米？（参考数据：