题目内容
已知：
=
=
=3，且b+d+f=0，求证：
=
=3．
| a |
| b |
| c |
| d |
| e |
| f |
| a+c |
| b+d |
| c+e |
| d+f |
考点：比例的性质
专题：
分析：根据已知
=
=
=3，可得a=3b，c=3d，e=3f，将其代入即可证明．
| a |
| b |
| c |
| d |
| e |
| f |
解答：证明：∵
=
=
=3，
∴a=3b，c=3d，e=3f，bdf≠0，
∵b+d+f=0，
∴b+d≠0，d+f≠0，
∴
=
=3，
=
=3，
∴
=
=3．
| a |
| b |
| c |
| d |
| e |
| f |
∴a=3b，c=3d，e=3f，bdf≠0，
∵b+d+f=0，
∴b+d≠0，d+f≠0，
∴
| a+c |
| b+d |
| 3b+3d |
| b+d |
| c+e |
| d+f |
| 3d+3f |
| d+f |
∴
| a+c |
| b+d |
| c+e |
| d+f |
点评：本题考查了比例的性质，是基础题，比较简单．
练习册系列答案
走进文言文系列答案
相关题目
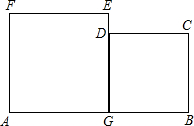如图所示，这是一块工厂的下脚料铁板，其中AGEF和BCDG都是正方形．某个体水箱加工生产户经过计算得知，这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积（切割，焊接过程中的面积不变），他思考了一会，决定购买这块下脚料用于焊接冰箱．请你利用所学的知识帮助他设计一种最简便的切割，焊接方法，并证明你的设计方案．
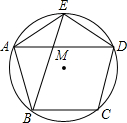如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点M．