题目内容
3. 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,过点O作EF⊥BD,与边AD、BC分别交于点E、F.求证:四边形BEDF是菱形.
如图,已知平行四边形ABCD的对角线AC与BD相交于点O,过点O作EF⊥BD,与边AD、BC分别交于点E、F.求证:四边形BEDF是菱形.
分析 由四边形ABCD是平行四边形,即可得AD∥BC,OB=OD,易证得△OED≌△OFB,可得DE=BF,即可证得四边形BEDF是平行四边形,又由EF⊥BD,即可证得平行四边形BEDF是菱形.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,
∵∠EDO=∠FBO,∠OED=∠OFB,
∴△OED≌△OFB(AAS),
∴DE=BF,
又∵ED∥BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴?BEDF是菱形.
点评 此题考查了平行四边形的判定与性质,菱形的判定以及全等三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
14.二元一次方程x+2y=10的所有正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列数中,属于无理数的是( )
| A. | $\sqrt{2.5}$ | B. | $\root{3}{-64}$ | C. | 1.5151151115 | D. | $\frac{7π}{2π}$ |
15.某产品每件成本150元,销售阶段每件产品的销售价x(元)与产品的月销售量y(件)之间的关系如下表:若月销售量是销售价的一次函数.
求:(1)求出月销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为240元时,每月的销售利润.
| x(元) | 180 | 200 | 220 | … |
| y (件) | 850 | 750 | 650 | … |
(2)求销售价定为240元时,每月的销售利润.
12.下列说法中正确的是( )
| A. | 两条射线所组成的图形叫角 | |
| B. | 角的大小与所画的角的边的长短无关 | |
| C. | 角的两边是两条线段 | |
| D. | 角的两边是两条直线 |
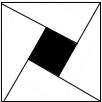 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为4-2$\sqrt{3}$.
由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为4-2$\sqrt{3}$. 如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n)
如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n) 如图,已知直线a∥b,点A在直线a上,点B、C在直线b上,点P在线段AB上,∠1=70°,∠2=100°,那么∠PCB=30度.
如图,已知直线a∥b,点A在直线a上,点B、C在直线b上,点P在线段AB上,∠1=70°,∠2=100°,那么∠PCB=30度.