题目内容
2.某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件;若销售单价每涨1元,每周销售量就减少10件.设销售单价为x元(x≥50),一周的销售量为y件.(1)求y与x之间的函数关系式(标明x取值范围);
(2)设一周的销售利润为W,写出W与x之间的函数关系式,若要获得最大利润,一周应进货多少件?
分析 (1)根据原有销售量减去减少的销售量即可列出;
(2)利用一周的销售量×每件销售利润=一周的销售利润列出二次函数,用配方法求得最值解决问题.
解答 解:(1)根据题意得y=500-10(x-50)=-10x+1000,(50≤x≤100);
(2)利润W=(x-40)(1000-10x),
=-10x2+1400x-40000,
=-10(x-70)2+9000,
当x=70时,获得最大利润,一周应进货y=1000-10x=300件.
点评 此题主要考查了二次函数的应用以及用配方法求出最大值,准确分析题意,列出W与x之间的二次函数关系式是解题关键.

练习册系列答案
相关题目
17.已知G为△ABC的重心,过G的直线交AB于P,交AC于Q,设$\frac{AP}{PB}$=a,$\frac{AQ}{QC}$=b,则$\frac{1}{a}$+$\frac{1}{b}$=1.
11.有下列各数:0.01,10,-$\frac{1}{3}$,-|-2|,-90,-(-3.5),其中属于负数的共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
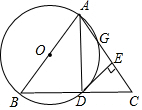 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证:
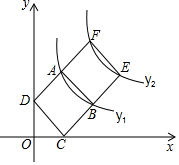 如图,在边长均为1的正方形ABCD和ABEF中,顶点A,B在双曲线y1=$\frac{{k}_{1}}{x}$(k1≠0)上,顶点E,F在双曲线y2=$\frac{{k}_{2}}{x}$(k2≠0)上,顶点C,D分别在x轴和y轴上,则k1=1,k2=3.
如图,在边长均为1的正方形ABCD和ABEF中,顶点A,B在双曲线y1=$\frac{{k}_{1}}{x}$(k1≠0)上,顶点E,F在双曲线y2=$\frac{{k}_{2}}{x}$(k2≠0)上,顶点C,D分别在x轴和y轴上,则k1=1,k2=3.