题目内容
15.任意实数a,可用[a]表示不超过a的最大整数,如[4]=4,[$\sqrt{3}$]=1,现对72进行如下操作:72→[$\sqrt{72}$]=8→[$\sqrt{8}$]=2→[$\sqrt{2}$]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据[a]表示不超过a的最大整数计算,可得答案.
解答 解:900→第一次[$\sqrt{900}$]=30→第二次[$\sqrt{30}$]=5→第三次[$\sqrt{5}$]=2→第四次[$\sqrt{2}$]=1,
即对数字900进行了4次操作后变为1.
故选:B.
点评 本题考查了估算无理数的大小的应用,主要考查学生的阅读能力和逆推思维能力.

练习册系列答案
相关题目
6.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.在实数0,$\frac{\sqrt{3}}{2}$,-3$\frac{1}{7}$,1.020020002,$\root{3}{4}$,-π中,无理数有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7. 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )
 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
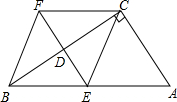 如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE,求证:四边形BEFC是菱形.
如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE,求证:四边形BEFC是菱形.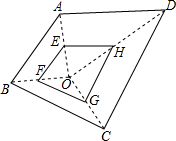 如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )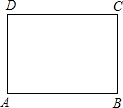 如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)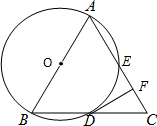 如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.
如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.