题目内容
8. 已知:如图,AC∥BD,AB∥CD,∠1=∠E,∠2=∠F,AE交CF于点O.求证:∠1与∠2互余.
已知:如图,AC∥BD,AB∥CD,∠1=∠E,∠2=∠F,AE交CF于点O.求证:∠1与∠2互余.
分析 首先由AC∥BD,可证得∠CAO=∠E,∠ACO=∠F,即可得:∠1=∠CAO=$\frac{1}{2}$∠BAC,∠2=∠ACO=$\frac{1}{2}$∠ACD,又由AB∥CD即可得出结论.
解答 证明:∵AC∥BD,
∴∠CAO=∠E,∠ACO=∠F,
∵∠1=∠E,∠2=∠F,
∴∠1=∠CAO=$\frac{1}{2}$∠BAC,∠2=∠ACO=$\frac{1}{2}$∠ACD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAO+∠ACO=90°,
∴∠1+∠2=90°,即∠1与∠2互余.
点评 此题考查了平行线的性质.解题的关键是仔细识图,数形结合思想的合理应用.

练习册系列答案
相关题目
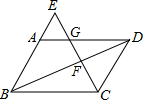 如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.
如图,已知?ABCD,点E是BA延长线上一点,CE与AD,BD分别相交于点G、F,求证:$\frac{CF}{GF}$=$\frac{EF}{CF}$.
 如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.
如图,这是一个小立方块所搭几何体的俯视图,正方形中的数字表示在该位置小立方块的个数.请你画出它的主视图和左视图.