题目内容
 在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG、BG、DG.求证:△DCG≌△BEG.
在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG、BG、DG.求证:△DCG≌△BEG.考点:矩形的性质,全等三角形的判定
专题:证明题
分析:先求出∠BAE=45°,判断出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AB=BE,∠AEB=45°,从而得到BE=CD,再求出△CEF是等腰直角三角形,根据等腰直角三角形的性质可得CG=EG,再求出∠BEG=∠DCG=135°,然后利用“边角边”证明即可.
解答:证明:∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
,
∴△DCG≌△BEG(SAS).
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
|
∴△DCG≌△BEG(SAS).
点评:本题考查了矩形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,难点在于证明得到△ABE和△CEF都是等腰直角三角形.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知等腰三角形的一边等于4,一边等于7,那么它的周长等于( )
| A、12 | B、18 |
| C、12或21 | D、15或18 |
 如图,AO交⊙O于点C,过⊙O上一点P,作PF⊥OA,垂足为F,直线PF交⊙O于点E,∠FPC=∠CPA,请问PA是⊙A的切线吗?为什么?
如图,AO交⊙O于点C,过⊙O上一点P,作PF⊥OA,垂足为F,直线PF交⊙O于点E,∠FPC=∠CPA,请问PA是⊙A的切线吗?为什么?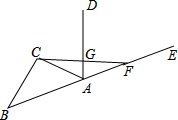 如图,已知△ABC,作△ABC的外角∠EAC的平分线AD,在射线AE上截取AF=AC,连接CF交AD于点G.试猜想AG与CF的位置关系,并证明你的猜想.
如图,已知△ABC,作△ABC的外角∠EAC的平分线AD,在射线AE上截取AF=AC,连接CF交AD于点G.试猜想AG与CF的位置关系,并证明你的猜想. 如图,点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足是E、F,点D为BC的中点.
如图,点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足是E、F,点D为BC的中点.