题目内容
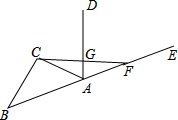如图，已知△ABC，作△ABC的外角∠EAC的平分线AD，在射线AE上截取AF=AC，连接CF交AD于点G．试猜想AG与CF的位置关系，并证明你的猜想．考点：等腰三角形的判定与性质
专题：
分析：根据等腰三角形的定义，可得△ACF的形状，根据等腰三角形的性质，可得答案．
解答：解：AG⊥CF，理由如下：
∵AF=AC，
∴△ACF是等腰三角形，
∵AD平分∠FAC，
∴AG是CF边上的高线，
即AG⊥CF．
∵AF=AC，
∴△ACF是等腰三角形，
∵AD平分∠FAC，
∴AG是CF边上的高线，
即AG⊥CF．
点评：本题考查了等腰三角形的判定与性质，利用了等腰三角形的判定与性质．
练习册系列答案
相关题目
运用分配律计算（-3）×（-8+2-3），有下列四种不同的结果，其中正确的是（ ）
| A、-3×8-3×2-3×3 |
| B、-3×（-8）-3×2-3×3 |
| C、（-3）×（-8）+3×2-3×3 |
| D、（-3）×（-8）-3×2+3×3 |
在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG、BG、DG．求证：△DCG≌△BEG．
有理数a、b、c在数轴上的位置如图所示，化简式子：|b|+|a-c|+|b-c|+|a-b|．
已知：如图，在△ABC中，D是AB上一点，且DA=DB=DC．求证：△ABC是直角三角形．