题目内容
 将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是( )
将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是( )| A、70° | B、50° |
| C、40° | D、30° |
考点:旋转的性质
专题:
分析:根据旋转可得AB=AD,∠BAD=∠CAE,然后根据等边对等角可得∠B=∠ADB=70°,再利用三角形内角和定理可以计算出∠BAD的度数,进而得到∠CAE的度数.
解答:解:根据旋转可得AB=AD,∠BAD=∠CAE,
∵AB=AD,∠B=70°,
∴∠B=∠ADB=70°,
∴∠BAD=180°-70°-70°=40°,
∴∠CAE=40°,
故选C.
∵AB=AD,∠B=70°,
∴∠B=∠ADB=70°,
∴∠BAD=180°-70°-70°=40°,
∴∠CAE=40°,
故选C.
点评:此题主要考查了旋转的性质,解题的关键是找出旋转后相等的线段和相等的角.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
下列四组图形中,不是相似图形的是( )
A、 |
B、 |
C、 |
D、 |
设a、b是方程x2+x-2014=0的两个实数根,则a2+2a+b的值为( )
| A、2014 | B、2013 |
| C、2012 | D、2011 |
 如图,在∠MON的两边上顺次取点,使 DE=CD=BC=AB=OA,若∠MON=20°,则∠NDE=
如图,在∠MON的两边上顺次取点,使 DE=CD=BC=AB=OA,若∠MON=20°,则∠NDE=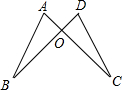 如图AC与BD交于O点,若OA=OD,要证明△AOB≌△DOC,
如图AC与BD交于O点,若OA=OD,要证明△AOB≌△DOC, 一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,车速不变,设慢车行驶t小时,两车相距S千米,S与t的关系如图所示,则慢车行驶
一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,车速不变,设慢车行驶t小时,两车相距S千米,S与t的关系如图所示,则慢车行驶 如图,请画出△ABC关于点O点为对称中心的对称图形.
如图,请画出△ABC关于点O点为对称中心的对称图形.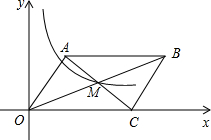 在直角坐标系中,?OCBA的边OC在x轴的正半轴上,点O为坐标原点,点B的坐标为(10,4),点M为对角线AC、OB的交点,反比例函数的图象经过点M,则该反比例函数的解析式为
在直角坐标系中,?OCBA的边OC在x轴的正半轴上,点O为坐标原点,点B的坐标为(10,4),点M为对角线AC、OB的交点,反比例函数的图象经过点M,则该反比例函数的解析式为