题目内容
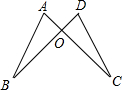 如图AC与BD交于O点,若OA=OD,要证明△AOB≌△DOC,
如图AC与BD交于O点,若OA=OD,要证明△AOB≌△DOC,(1)若以“ASA”为依据,需添加的条件是
(2)若以“SAS”为依据,需添加的条件是
(3)若以“AAS”为依据,需添加的条件是
考点:全等三角形的判定
专题:
分析:(1)全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件填上即可;
(2)全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件填上即可;
(3)全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件填上即可.
(2)全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件填上即可;
(3)全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件填上即可.
解答:解:(1)∵OA=OD,∠AOB=∠DOC,
∴当∠A=∠D时,符合ASA定理,
故答案为:∠A=∠D;
(2)∵OA=OD,∠AOB=∠DOC,
∴当OB=OC时,符合SAS定理,
故答案为:OB=OC;
(3)∵OA=OD,∠AOB=∠DOC,
∴当∠B=∠C时,符合AAS定理,
故答案为:∠B=∠C.
∴当∠A=∠D时,符合ASA定理,
故答案为:∠A=∠D;
(2)∵OA=OD,∠AOB=∠DOC,
∴当OB=OC时,符合SAS定理,
故答案为:OB=OC;
(3)∵OA=OD,∠AOB=∠DOC,
∴当∠B=∠C时,符合AAS定理,
故答案为:∠B=∠C.
点评:本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了1000次,其中有125次摸到白球,因此小亮估计口袋中的红球大约有( )个.
| A、100个 | B、90个 |
| C、80个 | D、70个 |
 将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是( )
将△ABC绕点A逆时针旋转一定的角度后,得到△ADE,且点B的对应点D恰好落在BC边上,若∠B=70°,则∠CAE的度数是( )| A、70° | B、50° |
| C、40° | D、30° |