题目内容
 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB.①求证:BC•AF=BF•DE;
②若∠AED=30°,AB=5
| 3 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:证明题
分析:(1)求三角形相似就要得出两组对应的角相等,已知了∠BFE=∠C,根据等角的补角相等可得出∠ADE=∠AFB,根据AB∥CD可得出∠BAF=∠AED,这样就构成了两三角形相似的条件.
(2)根据△ABF∽△EAD得到
=
,根据∠AED=30°、AB=5
得到BE=5,AE=10代入即可解得:ED=2
,从而得到CE=3
.
(2)根据△ABF∽△EAD得到
| AB |
| AE |
| AF |
| ED |
| 3 |
| 3 |
| 3 |
解答:(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
∴
=
即:AD•AF=BF•DE
∵AD=BC
∴BC•AF=BF•DE.
(2)∵△ABF∽△EAD
∴
=
∵∠AED=30°,
∴∠BAE=30°,
∵AB=5
,
∴BE=5,AE=10,
即:
=
解得:ED=2
∴CE=3
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
∴
| AD |
| BF |
| DE |
| AF |
即:AD•AF=BF•DE
∵AD=BC

∴BC•AF=BF•DE.
(2)∵△ABF∽△EAD
∴
| AB |
| AE |
| AF |
| ED |
∵∠AED=30°,
∴∠BAE=30°,
∵AB=5
| 3 |
∴BE=5,AE=10,
即:
5
| ||
| 10 |
| 3 |
| ED |
解得:ED=2
| 3 |
∴CE=3
| 3 |
点评:本题考查了相似三角形的判定与性质,解题的关键是根据平行四边形的性质得到相等的角和相等的线段.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设a=
-1,则代数式a2+2a-10的值为( )
| 7 |
| A、-3 | ||
| B、-4 | ||
C、-4
| ||
D、-4
|
方程(3x-1)(2x+4)=1的解是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
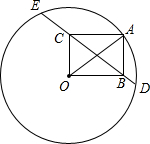 如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是
如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是