题目内容
已知多项式x2+7xy+my2-5x+43y-24可分解成x、y的两个一次因式,则实数m= .
考点:因式分解的意义
专题:
分析:根据x2项的系数是1,x一次方项的系数是-5,所以把-24分解成3×(-8),然后据已知条件设出这两个一次因式分别是x+ay+3与x+by-8,相乘后根据多形式相等,对应项的系数相等列出方程组求出a、b的值,从而得到答案.
解答:解:设x2+7xy+my2-5x+43y-24=(x+ay+3)(x+by-8),
∵(x+ay+3)(x+by-8)=x2+(a+b)xy+aby2-5x+(-8a+3b)y-24,
∴x2+7xy+my2-5x+43y-24=x2+(a+b)xy+aby2-5x+(-8a+3b)y-24,
∴
,
解得
,
∴m=ab=(-2)×9=-18.
故答案为:-18.
∵(x+ay+3)(x+by-8)=x2+(a+b)xy+aby2-5x+(-8a+3b)y-24,
∴x2+7xy+my2-5x+43y-24=x2+(a+b)xy+aby2-5x+(-8a+3b)y-24,
∴
|
解得
|
∴m=ab=(-2)×9=-18.
故答案为:-18.
点评:本题考查了因式分解的意义;设出这两个一次因式分别是x+ay+3与x+by-8,是正确解答本题的关键.

练习册系列答案
相关题目
若要使分式
的值为0,则x的值应为( )
| x2-9 |
| x+3 |
| A、x=3 | B、x=-3 |
| C、x=±3 | D、x≠-3 |
小明记录了长春市今年2月8日至2月13日的最低气温分别为-20℃,-20℃,-17℃,-14°C,-14℃,-20℃,最低气温的众数为( )
| A、-14℃ | B、-17℃ |
| C、-20℃ | D、-18.5℃ |
 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠C=∠EFB. 如图,梯形ABCD中,EF过对角线的交点O,且AD∥EF∥BC,AD=m,BC=n,则EF长为
如图,梯形ABCD中,EF过对角线的交点O,且AD∥EF∥BC,AD=m,BC=n,则EF长为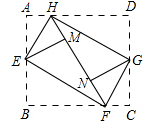 如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AH:HD=
如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AH:HD= 如图,在?ABCD中,E是CD上的一个动点(不与C、D重合),BE的延长线交AD的延长线于点F,则图中共有
如图,在?ABCD中,E是CD上的一个动点(不与C、D重合),BE的延长线交AD的延长线于点F,则图中共有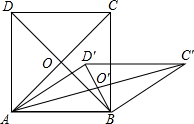 已知正方形ABCD的边长为1,O为其对角线交点,若保持AB不动,将正方形向顺时针方向压扁,得到菱形ABC′D′(如图).若∠BAD′=30°,则点O运动的路程为( )
已知正方形ABCD的边长为1,O为其对角线交点,若保持AB不动,将正方形向顺时针方向压扁,得到菱形ABC′D′(如图).若∠BAD′=30°,则点O运动的路程为( )