题目内容
1.一个两位数,个位数字是a.(1)当两位数的十位数字和个位数字的和是5时,求这个两位数(用含a的代数式表示);
(2)“如果两位数的个位数字与十位数字的和能够被3整除,那么这个两位数一定能被3整除”.这句话正确吗?请说明理由.
分析 (1)根据题题可以表示出十位数字,从而可以表示出这个两位数;
(2)根据两位数的个位数字与十位数字的和能够被3整除,和第一问的提示可以表示出这个两位数,从而可以推得结论成立.
解答 解:(1)根据题意可得,十位数字为:5-a.
则这个两位数可以表示为:10×(5-a)+a=50-10a+a=50+9a.
即这个两位数可表示为:50+9a.
(2)正确.
理由:设这个两位数为xa,则$\frac{x+a}{3}=n$(n为整数).
∵xa=10x+a,$\frac{x+a}{3}=n$,
∴x=3n-a.
∴10x+a=10(3n-a)+a=30n-9a.
∵30n-9a一定能被3整除,
∴这个两位数一定能被3整除.
点评 本题考查列代数式,解题的关键是根据题意找出所求问题需要的条件.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
9.化简$\sqrt{-{a}^{3}}$•$\sqrt{\frac{1}{{a}^{2}}}$(a<0)得( )
| A. | $\sqrt{-a}$ | B. | -$\sqrt{a}$ | C. | -$\sqrt{-a}$ | D. | $\sqrt{a}$ |
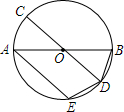 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.
如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE. 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程 的两个根.
的两个根.  的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由. 面积S最大时,求m的值.
面积S最大时,求m的值.