题目内容
9.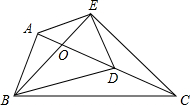 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.(1)求证:BE=CE;
(2)延长CE、BA交于F,设BE与AC相交于点O,则OE与EF的关系应为OE=OF;
(3)在(2)的条件下,已知AF=2,AO=1,求AB的长.
分析 (1)欲证明BE=EC,只要证明△EAB≌△EDC即可.
(2)欲证明BE=EC,只要证明△BEF≌△CEO即可.
(3)设AB=x,根据AC=2AB列出方程即可解决.
解答 (1)证明:在图1中, ∵EA=ED,∠AED=90°,
∵EA=ED,∠AED=90°,
∴∠EAD=∠EDA=45°,
∴∠EDC=180°-∠EDA=135°,
∵∠BAC=90°,
∴∠BAE=∠BAC+∠EAD=135°,
∴∠EAB=∠EDC,
∵AC=2AB,DA=DC,
∴AB=DC,
在△EAB和△EDC中,
$\left\{\begin{array}{l}{EA=ED}\\{∠EAB=∠EDC}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△EDC,
∴BE=EC.
(2)在图2中,由(1)可知△EAB≌△EDC,
∴BE=EC,∠ABE=∠ECD,
在△BEF和△CEO中,
$\left\{\begin{array}{l}{∠FBE=∠ECO}\\{BE=EC}\\{∠BEF=∠CEO}\end{array}\right.$,
∴△BEF≌△CEO,
∴EF=OE.
故答案为EF=OE.
(3)由(2)可知△BEF≌△CEO,设AB=x,
∵AF=2,AO=1,
∴BF=CO=AB+AF=x+2,AC=AO+OC=1+x+2=x+3,
∵AC=2AB,
∴x+3=2x
∴x=3,
∴AB=3.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、解题的关键是正确寻找全等三角形,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
7.若二次函数y=(a-$\sqrt{3}$)x2的图象开口向下,则a的取值范围为( )
| A. | a>$\sqrt{3}$ | B. | a<$\sqrt{3}$ | C. | a>-$\sqrt{3}$ | D. | a<-$\sqrt{3}$ |
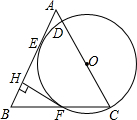 如图,△ABC中,AB=AC.D为AC上一点.以CD为直径的⊙O与AB边相切于点E.与BC交于点F.FH⊥AB于H,求证:EH=$\frac{1}{2}$CD.
如图,△ABC中,AB=AC.D为AC上一点.以CD为直径的⊙O与AB边相切于点E.与BC交于点F.FH⊥AB于H,求证:EH=$\frac{1}{2}$CD. 用一个平面按如图所示的方式“切割”正方体,可以得到一个正方形的截面,将该正方体的侧面展开,“切割线”(虚线)位置正确的是( )
用一个平面按如图所示的方式“切割”正方体,可以得到一个正方形的截面,将该正方体的侧面展开,“切割线”(虚线)位置正确的是( )



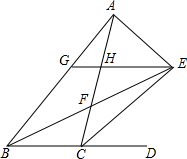 如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论:
如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论: