题目内容
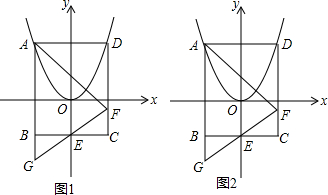
1.在四边形ABCD中,AD∥BC,AB=CD,∠B=45°,E为BC边上的一点,连接EA,作∠AEF,使得∠AEF=∠B,射线EF与CD交于点F.若AD=1,BC=5,且△ABE为等腰三角形,AB为一腰,则CF的长为5-2$\sqrt{2}$.分析 由等腰三角形的性质可得出∠BAE=∠BEA和AB=BE,再利用角与角的关系能求出∠CEF=∠BEA=67.5°,由三角形的内角和为180°可找出∠CEF=∠CFE,从而得出△CEF为等腰三角形,要求CF只需求出CE即可,由四边形ABCD为等腰梯形且AD=1,BC=5,∠B=45°,能够得出AB的值,到此,即可根据CF=CE=BC-AB得出结论.
解答 解:过点A作AH⊥BC于H,如图所示.
∵AD∥BC,AB=CD,
∴四边形ABCD是等腰梯形,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∴AH=BH=$\frac{BC-AD}{2}$=2,AB=$\sqrt{2}$BH=2$\sqrt{2}$.
又∵△△ABE为等腰三角形,
∴∠BAE=∠BEA,AB=BE,
∴BE=AB=2$\sqrt{2}$,CE=BC-BE=5-2$\sqrt{2}$,
∴∠AEB=$\frac{180°-∠B}{2}$=67.5°,
∴∠CEF=180°-∠AEB-∠AEF=67.5°.
∵∠CFE=180°-∠C-∠CEF=67.5°,
∴∠CEF=∠CFE,
∴△CEF是等腰三角形,
∴CF=CE=5-2$\sqrt{2}$.
故答案为:5-2$\sqrt{2}$.
点评 本题考查了等腰三角形的性质以及等腰直角三角形的性质,解题的关键是:找到∠CEF=∠CFE,即得出CF=CE,将求CF的长转化为求CE的长.本题难度不大,在计算中只要细心的寻找角与角之间的关系,利用等腰三角形的底角相等以及三角形内角和为180°,再借助巧分平角找出两角相等,从而得出等腰三角形.

练习册系列答案
相关题目
13.已知点P1(a-1,4)和P2(2,b)关于x轴对称,则(a+b)2015的值为( )
| A. | 72014 | B. | 1 | C. | -1 | D. | (-3)2014 |
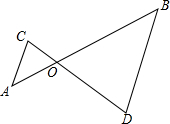 如图,AB和CD相交于O,∠A=∠B,试说明必有∠C=∠D.
如图,AB和CD相交于O,∠A=∠B,试说明必有∠C=∠D.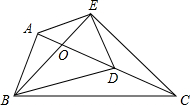 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE.