题目内容
1.(1)计算:$\frac{{x}^{2}}{x-1}$-x-1(2)先化简,再求值:($\frac{3x}{x-2}-\frac{x}{x+2}$)÷$\frac{x}{{x}^{2}-4}$,在-2,0,3,2四个数中选一个合适的代入求值.
分析 (1)先通分,再把分子相加减即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=$\frac{{x}^{2}}{x-1}$-$\frac{(x+1)(x-1)}{x-1}$
=$\frac{{x}^{2}-{x}^{2}+1}{x-1}$
=$\frac{1}{x-1}$;
(2)原式=$\frac{3x(x+2)-x(x-2)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$
=$\frac{3{x}^{2}+6x-{x}^{2}+2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$
=$\frac{2{x}^{2}+8x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$
=$\frac{2x(x+4)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{x}$
=2x+8,
当x=3时,原式=6+8=14.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
11.已知点P关于y轴的对称点P1的坐标是(2,3),则点P坐标是( )
| A. | (-3,-2) | B. | (-2,3) | C. | (2,-3) | D. | (3,-2) |
12.用一个平面截去正方体的一个角,则截面不可能是( )
| A. | 等腰直角三角形 | B. | 等腰三角形 | C. | 锐角三角形 | D. | 等边三角形 |
9.某超市的一种饮料原价为x元,因为销量不错,涨价10%后再涨价10%,一段时间后销量下降,决定降价20%促销,降价后这种饮料的价格为( )
| A. | 0.9x元 | B. | 0.968x元 | C. | x元 | D. | 0.972x元 |
6.小王利用计算机设计了一个计算程序,输入和输出的数据如表:
如表输入的数据记为x,输出的数据记为y,则y与x满足的关系式为y=$\frac{2}{x+2}$.
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{2}{3}$ | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{1}{3}$ | $\frac{2}{7}$ | … |
13.如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )
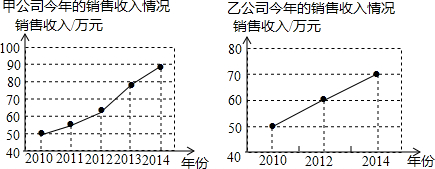

| A. | 甲公司近年的销售收入增长速度比乙公司快 | |
| B. | 乙公司近年的销售收入增长速度比甲公司快 | |
| C. | 甲、乙两公司近年的销售收入增长速度一样快 | |
| D. | 不能确定甲、乙两公司近年销售收入增长速度的快慢 |