题目内容
7.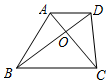 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果AO:AC=2:5,那么S△AOD:S△BOC为( )| A. | 4:25 | B. | 4:9 | C. | 2:5 | D. | 2:3 |
分析 首先根据AO:AC=2:5,可得OA:OC;然后根据相似三角形的面积的比的等于它们的相似比的平方,求出S△AOD:S△BOC是多少即可.
解答 解:∵在梯形ABCD中,AD∥BC,而且AO:AC=2:5,
∴OA:OC=2:3;
∵AD∥BC,
∴△AOD~△BOC,
∵OA:OC=2:3,
∴S△AOD:S△BOC=4:9.
故选:B
点评 此题主要考查了相似三角形的判定与性质的应用,以及梯形的特征和应用,要熟练掌握.

练习册系列答案
相关题目
15. 如左图所示的正三棱柱,其主视图正确的为( )
如左图所示的正三棱柱,其主视图正确的为( )
 如左图所示的正三棱柱,其主视图正确的为( )
如左图所示的正三棱柱,其主视图正确的为( )| A. |  | B. |  | C. |  | D. |  |
2.已知一次函数y1=-ax+3(a为常数)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象在第三相交于点A(a,$\frac{a}{2}$),则y2的解析式是( )
| A. | ${y_2}=\frac{9}{8x}$ | B. | ${y_2}=\frac{1}{2x}$ | C. | ${y_2}=\frac{2}{x}$ | D. | ${y_2}=-\frac{2}{x}$ |
12.2016年我国启动了新一代“E级超算”(计算速度达到每秒100亿亿次)样机系统的研制,预计今年底能够研制成功,这比美国计划在2025年造出“E级超算”提早8年,“E级超算”的计算速度用科学记数法表示为( )
| A. | 1.0×1017 | B. | 1.0×1018 | C. | 1.0×1019 | D. | 1.0×1020 |
19.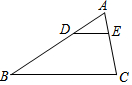 如图,在△ABC中,点D,E分别在AB,AC上,且$\frac{AD}{BD}=\frac{AE}{EC}=\frac{1}{2}$,则S△ADE:S△ABC( )
如图,在△ABC中,点D,E分别在AB,AC上,且$\frac{AD}{BD}=\frac{AE}{EC}=\frac{1}{2}$,则S△ADE:S△ABC( )
 如图,在△ABC中,点D,E分别在AB,AC上,且$\frac{AD}{BD}=\frac{AE}{EC}=\frac{1}{2}$,则S△ADE:S△ABC( )
如图,在△ABC中,点D,E分别在AB,AC上,且$\frac{AD}{BD}=\frac{AE}{EC}=\frac{1}{2}$,则S△ADE:S△ABC( )| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:9 |
16.2017年1月29日,宁波雅戈尔动物园发生老虎咬人事件,引发人们对“遵守规则”的热议.“动物园老虎咬人,应怪不守规则”,百度为你找到相关结果约368000个,其中368000用科学记数法表示为( )
| A. | 3.68×104 | B. | 3.68×105 | C. | 3.68×106 | D. | 36.8×104 |
 正方形ABCD中,点P是对角线BD的中点,过P点的直线分别交边AD,BC于M,N,EP⊥MN交边AB于点E.
正方形ABCD中,点P是对角线BD的中点,过P点的直线分别交边AD,BC于M,N,EP⊥MN交边AB于点E.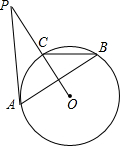 如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧$\widehat{CBA}$上一点,若∠ABC=32°,则∠P=( )度.
如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧$\widehat{CBA}$上一点,若∠ABC=32°,则∠P=( )度.