题目内容
12．
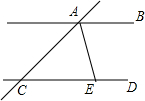如图，直线AB∥CD，AE平分∠CAB，AE与CD相交于点E，∠ACD=40°，则∠DEA=（ ）| A． | 40° | B． | 110° | C． | 70° | D． | 140° |
分析 先由平行线性质得出∠ACD与∠BAC互补，并根据已知∠ACD=40°计算出∠BAC的度数，再根据角平分线性质求出∠BAE的度数，进而得到∠DEA的度数．
解答 解：∵AB∥CD，
∴∠ACD+∠BAC=180°，
∵∠ACD=40°，
∴∠BAC=180°-40°=140°，
∵AE平分∠CAB，
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×140°=70°，
∴∠DEA=180°-∠BAE=110°．
故选B．
点评 本题考查了平行线的性质和角平分线的定义，做好本题要熟练掌握两直线平行，同旁内角互补．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
2．已知一次函数y1=-ax+3（a为常数）的图象与反比例函数y2=$\frac{k}{x}$（k≠0）的图象在第三相交于点A（a，$\frac{a}{2}$），则y2的解析式是（ ）
| A． | ${y_2}=\frac{9}{8x}$ | B． | ${y_2}=\frac{1}{2x}$ | C． | ${y_2}=\frac{2}{x}$ | D． | ${y_2}=-\frac{2}{x}$ |
3．若△ABC∽△A′B′C′，且△ABC与△A′B′C′的相似比为1：2，则△ABC与△A′B′C′的面积比是（ ）
| A． | 1：1 | B． | 1：2 | C． | 1：3 | D． | 1：4 |
20．若二次根式$\sqrt{a-4}$有意义，则a的取值范围是（ ）
| A． | a≥4 | B． | a≤4 | C． | a＞4 | D． | a＜4 |
7．下列事件中是随机事件的是（ ）
| A． | 三角形的内角和是180° | B． | 直径所对的圆周角是100° | ||
| C． | 若x2=4，则x=±2 | D． | 抛物线与x轴有2个交点 |
4．
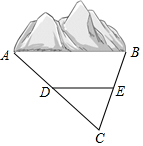某地需要开辟一条笔直隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使C到A，B两点均可直接到达，测量找到AC和BC的中点D，E，测得DE的长为1 100m，则隧道AB的长度为（ ）
某地需要开辟一条笔直隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使C到A，B两点均可直接到达，测量找到AC和BC的中点D，E，测得DE的长为1 100m，则隧道AB的长度为（ ）| A． | 3 300 m | B． | 2 200 m | C． | 1 100 m | D． | 550 m |
1．
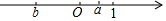已知实数a、b在数轴上的位置如图所示，则下列等式成立的是（ ）
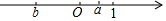已知实数a、b在数轴上的位置如图所示，则下列等式成立的是（ ）| A． | |a+b|=a+b | B． | |a+b|=a-b | C． | |a+1|=a+1 | D． | |b+1|=b+1 |
在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的横坐标是（ ）