题目内容
5.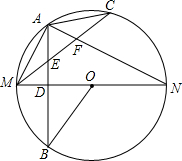 如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为$\widehat{AN}$上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:
如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为$\widehat{AN}$上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③$\widehat{AM}$=$\widehat{BM}$;④∠ACM+∠ANM=∠MOB;⑤AE=$\frac{1}{2}$MF.
其中正确结论的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据AB⊥MN,垂径定理得出①③正确,利用MN是直径得出②正确,$\widehat{AC}$=$\widehat{AM}$=$\widehat{BM}$,得出④正确,结合②④得出⑤正确即可.
解答 解:∵MN是⊙O的直径,AB⊥MN,
∴AD=BD,$\widehat{AM}$=$\widehat{BM}$,∠MAN=90°(①②③正确)
∵$\widehat{AC}$=$\widehat{AM}$,
∴$\widehat{AC}$=$\widehat{AM}$=$\widehat{BM}$,
∴∠ACM+∠ANM=∠MOB(④正确)
∵∠MAE=∠AME,
∴AE=ME,∠EAF=∠AFM,
∴AE=EF,
∴AE=$\frac{1}{2}$MF(⑤正确).
正确的结论共5个.
故选:D.
点评 此题考查圆周角定理,垂径定理,以及直角三角形斜边上的中线等于斜边的一半等知识.

练习册系列答案
相关题目
16.合肥地铁一号线工程将于2016年竣工,通车后城市交通通行和转换能力将成倍增长.该工程投资预算约为164亿元,这一数据用科学记数法表示为( )
| A. | 1.64×102元 | B. | 1.64×1010元 | C. | 1.64×109元 | D. | 1.64×108元 |
20.抛物线y=x2-4x+3的图象向左平移2个单位长度后所得新的抛物线的顶点坐标为( )
| A. | (0,-1) | B. | (0,-3) | C. | (-2,-3) | D. | (-2,-1) |
10.以下事件中,不可能发生的是( )
| A. | 打开电视,正在播广告 | |
| B. | 地球绕着月亮转 | |
| C. | 掷一次骰子,向上一面是2点 | |
| D. | 经过某一有交通信号灯的路口,遇到红灯 |
17.下列运算正确的是( )
| A. | a+a3=a4 | B. | (a+b)2=a2+b2 | C. | a10÷a2=a5 | D. | (a2)3=a6 |