题目内容
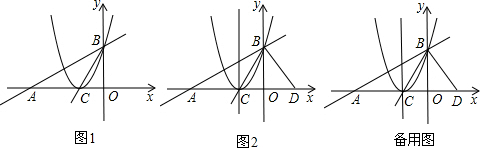
5.已知:如图1,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴,y轴的交点分别为A,B,将∠OBA对折,折痕交x轴于点C,一过点B的抛物线顶点恰好在点C.(1)直接写出点C的坐标,并求出抛物线的解析式:
(2)Q为线段BC上一点,请求出|QA-QO|的取值范围;
(3)在x轴上有一点D(1,0),连接BD,在△BCD中有一点E,E点到△BCD各顶点的距离相等,直线DE交抛物线的对称轴于点F.
①在图2中作出点E和点F,并求出点E的坐标;
②当x>-1时,在直线CE和抛物线上是否分别存在点M和点N,使四边形FCMN为特殊梯形?若存在,求点M,N的坐标;若不存在,说明理由.
分析 (1)先根据题意,根据坐标轴上点的坐标特征得到A,B点的坐标,进一步得到OA,OB的长,根据三角函数得到点C的坐标,再根据待定系数法求出抛物线的解析式;
(2)求出AB-BO,AC-OC的值,即可求出|QA-QO|的取值范围;
(3)①先得到△BCD是等边三角形,再根据三角形重心的定义即可得到点E的坐标;
②分两种情况讨论得到四边形FCMN为等腰梯形或四边形FCMN为直角梯形.
解答 解:(1)当x=0时,y=$\frac{\sqrt{3}}{3}$×0+$\sqrt{3}$=$\sqrt{3}$;
当y=0时,0=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,解得x=3;
则A(-3,0),B(0,$\sqrt{3}$),
OA=3,OB=$\sqrt{3}$,
∴tan∠ABO=$\frac{OA}{OB}$=$\sqrt{3}$,
∴∠ABO=60°,
由折叠的性质可知,∠CBO=30°,
∴OC=BO•tan∠CBO=1,
∴C(-1,0),
设抛物线解析式为y=a(x+1)2,依题意有a(0+1)2=$\sqrt{3}$,解得a=$\sqrt{3}$.
故抛物线的解析式为y=$\sqrt{3}$(x+1)2=$\sqrt{3}$x2+2$\sqrt{3}$x+$\sqrt{3}$;
(2)∵AB-BO=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$-$\sqrt{3}$=$\sqrt{3}$,
AC-OC=(3-1)-1=1,
∴1≤|QA-QO|≤$\sqrt{3}$;
(3)①如图2所示: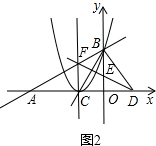
∵BC=CD=BD=2,
∴△BCD是等边三角形,
∴E(0,$\frac{\sqrt{3}}{3}$);
②当M1(-$\frac{1}{3}$,$\frac{2\sqrt{3}}{9}$),N1(-$\frac{1}{3}$,$\frac{4\sqrt{3}}{9}$)和M2(1,$\frac{2\sqrt{3}}{3}$),N2(0,$\sqrt{3}$)(与点B重合)时,四边形FCMN为等腰梯形;
当M3($\frac{\sqrt{6}}{3}$-1,$\frac{\sqrt{2}}{3}$),N3($\frac{\sqrt{6}}{3}$-1,$\frac{2\sqrt{3}}{3}$)和M4($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),N4(0,$\sqrt{3}$)(与点B重合)时,四边形FCMN为直角梯形.
点评 考查了二次函数综合题,涉及的知识点有:坐标轴上点的坐标特征,三角函数,待定系数法求抛物线的解析式,等边三角形的判定和性质,梯形的性质,分类思想的应用,综合性较强,有一定的难度.

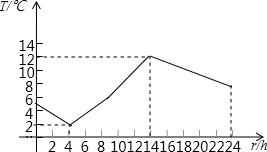 如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )| A. | 10℃ | B. | -10℃ | C. | 8℃ | D. | 12℃ |
 如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.
如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.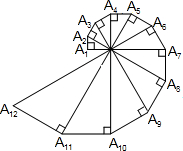 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.