题目内容
7.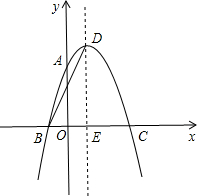 如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由.
分析 (1)将A、B两点坐标代入即可求得解析式;
(2)先求出D点坐标,从而求出BE、DE、BD长度,cos∠DBE则可直接算出;
(3)由于B是公共点,不可能是直角顶点,所以就只剩下两种情,即让C和F分别为直角顶点,根据相似性质,列出比例等式计算即可.
解答 解:(1)将A(0,3)、B(-1,0)代入y=ax2+2x+c可得:
c=3,a=-1,
抛物线的解析式为y=-x2+2x+3,
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4),
∴BE=2,DE=4,
∴BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=2$\sqrt{5}$,
∴cos∠DBE=$\frac{BE}{BD}$=$\frac{\sqrt{5}}{5}$;
(3)∵B(-1,0),D(1,4),
∴直线BD的解析式为y=2x+2,
∵y=-x2+2x+3=-(x-3)(x+1),
∴C(3,0),
∴BC=4,
①若△BED∽△BFC,如图1,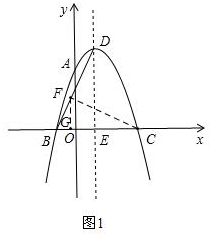
则∠BED=∠BFC=90°,
作FG⊥BC于G,
∵cos∠CBF=$\frac{BF}{BC}=\frac{\sqrt{5}}{5}$,
∴BF=$\frac{4\sqrt{5}}{5}$,
∴BG=$\frac{\sqrt{5}}{5}BF$=$\frac{4}{5}$,
∴OG=$\frac{1}{5}$,GF=$\frac{8}{5}$,
∴F(-$\frac{1}{5}$,$\frac{8}{5}$);
②若△BED∽△BCF,如图2,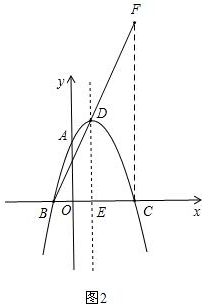
则∠BCF=90°,
∴F点横坐标为3,
将3代入BD解析式得:y=8,
∴F(3,8);
综上所述,满足要求的F点的坐标为:(-$\frac{1}{5}$,$\frac{8}{5}$)、(3,8).
点评 本题考查了待定系数法求抛物线解析式、锐角三角函数、相似三角形的判断与性质等重要知识点,难度不大.第(2)的关键是找到∠DBE所在直角三角形,求出邻边与斜边;对于第(3)问,首注意到要求相似的两个三角形有公共点B,这样就只有两种情况,并且∠BED是直角,这样就只需通过作垂线找到F点.

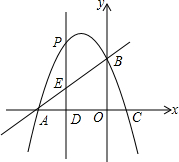 在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.
在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.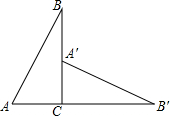 如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.
如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.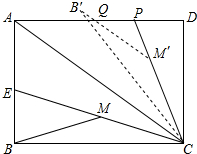 已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.