题目内容
3.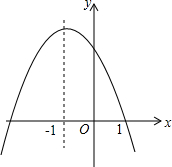 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,给出以下结论:①a+b+c<0;②c-a>0;③a-2b+4c>0;④m(am+b)+b<a(m≠-1),其中正确的结论的个数是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,给出以下结论:①a+b+c<0;②c-a>0;③a-2b+4c>0;④m(am+b)+b<a(m≠-1),其中正确的结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解 :①如图所示:当x=1时,y=0,则a+b+c=0,故①错误;
:①如图所示:当x=1时,y=0,则a+b+c=0,故①错误;
②如图所示:抛物线开口方向向下,则a<0.
抛物线与y轴交于正半轴,则c>0,
所以c-a>0,故②正确;
③如图所示:抛物线对称轴为x=-$\frac{b}{2a}$=-1,则b=2a.
所以a+b+c=3a+c=0,则c=-3a.
所以a-2b+4c=-3a-12a=-15a>0即a-2b+4c>0,故③正确;
④抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2+bm+c≤a-b+c(m为任意实数),
∴m(am+b)≤a-b(m为任意实数),
即:m(am+b)+b<a(m≠-1),
故④正确.
综上所述,正确的结论有3个.
故选:C.
点评 主要考查图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.“十一”节期间,某商品按成本价提高30%后标价,再打8折(标价的80%)销售,售价为240元.设该商品的成本价为x元,根据题意,下面所列方程正确的是( )
| A. | x•30%•80%=240 | B. | x•(1+30%)•80%=240 | ||
| C. | x•(1+30%)•(1-80%)=240 | D. | x•30%=240•80% |
18.三角形的角平分线是( )
| A. | 直线 | B. | 线段 | C. | 射线 | D. | 无法确定 |
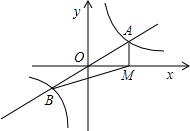 如图,直线y=mx与双曲线$y=\frac{k}{x}$交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若S△ABM=4,则k的值是( )
如图,直线y=mx与双曲线$y=\frac{k}{x}$交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若S△ABM=4,则k的值是( )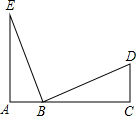 如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件AE=CB,使得△EAB≌△BCD,理由是SAS.
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件AE=CB,使得△EAB≌△BCD,理由是SAS.