题目内容
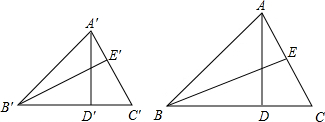 如图,AD、BE是△ABC的两条高,A′D′、B′E′是△A′B′C′的两条高,△ABD∽△A′B′D′,∠C=∠C′,求证:
如图,AD、BE是△ABC的两条高,A′D′、B′E′是△A′B′C′的两条高,△ABD∽△A′B′D′,∠C=∠C′,求证:| AD |
| A′D′ |
| BE |
| B′E′ |
考点:相似三角形的性质
专题:证明题
分析:根据相似三角形对应角相等可得∠ABC=∠A′B′C′,∠BAC=∠B′A′C′,然后求出△ABD和△A′B′D′相似,再根据相似三角形对应边成比例可得
=
,同理求出△ABE和△A′B′E′相似,再根据相似三角形对应边成比例可得
=
,然后等量代换即可得证.
| AD |
| A′D′ |
| AB |
| A′B′ |
| BE |
| B′E′ |
| AB |
| A′B′ |
解答:证明:∵△ABD∽△A′B′D′,
∴∠ABC=∠A′B′C′,∠BAC=∠B′A′C′,
∵AD是△ABC的高,A′D′是△A′B′C′的,
∴∠ADB=∠A′D′B′=90°,
∴△ABD∽△A′B′D′,
∴
=
,
同理可求△ABE∽△A′B′E′,
∴
=
,
∴
=
.
∴∠ABC=∠A′B′C′,∠BAC=∠B′A′C′,
∵AD是△ABC的高,A′D′是△A′B′C′的,
∴∠ADB=∠A′D′B′=90°,
∴△ABD∽△A′B′D′,
∴
| AD |
| A′D′ |
| AB |
| A′B′ |
同理可求△ABE∽△A′B′E′,
∴
| BE |
| B′E′ |
| AB |
| A′B′ |
∴
| AD |
| A′D′ |
| BE |
| B′E′ |
点评:本题考查了相似三角形的性质,相似三角形的判定,熟练掌握三角形相似的判定方法是解题的关键,难点在于根据相似三角形对应角相等再求出两条对应高所在的三角形相似.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,在△ABC中,AB=AC=10,AD是角平分线,AD=6,则BC的长度为( )
如图,在△ABC中,AB=AC=10,AD是角平分线,AD=6,则BC的长度为( )| A、6 | B、8 | C、12 | D、16 |
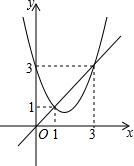 函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )
函数y1=ax2+bx+c与y2=x的图象如图所示,当y1<y2时,自变量x的取值范围是( )| A、1<x<3 | B、x<1 |
| C、x>3 | D、x<1或x>3 |
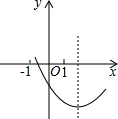 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是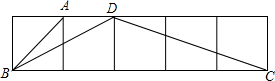 如图所示,点A、B、C、D在正方形网格的格点上,求∠BDC的度数.
如图所示,点A、B、C、D在正方形网格的格点上,求∠BDC的度数.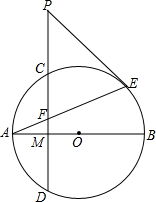 如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?
如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?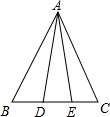 已知:如图,在△ABC中,D、E是BC上两点,且AD=AE,∠BAD=∠EAC,求证:AB=AC.
已知:如图,在△ABC中,D、E是BC上两点,且AD=AE,∠BAD=∠EAC,求证:AB=AC.