题目内容
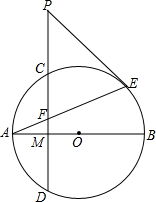 如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?
如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?考点:切线的性质
专题:常规题型
分析:连接OE,根据切线的性质,由PE是⊙O的切线得到OE⊥PE,则∠1+∠2=90°;由于M是CD的中点,根据垂径定理的推理得到OA⊥CD,所以∠A+∠3=90°,
加上∠1=∠A,利用等角的余角相等得到∠2=∠3,而∠3=∠4,所以∠2=∠4,于是根据等腰三角形的判定即可得到PE=PF.
加上∠1=∠A,利用等角的余角相等得到∠2=∠3,而∠3=∠4,所以∠2=∠4,于是根据等腰三角形的判定即可得到PE=PF.
解答:解: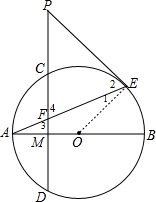 PE=PF.理由如下:
PE=PF.理由如下:
连接OE,如图,
∵PE是⊙O的切线,
∴OE⊥PE,
∴∠1+∠2=90°,
∵M是CD的中点,
∴OA⊥CD,
∴∠A+∠3=90°,
而OA=OE,
∴∠1=∠A,
∴∠2=∠3,
而∠3=∠4,
∴∠2=∠4,
∴PE=PF.
 PE=PF.理由如下:
PE=PF.理由如下:连接OE,如图,
∵PE是⊙O的切线,
∴OE⊥PE,
∴∠1+∠2=90°,
∵M是CD的中点,
∴OA⊥CD,
∴∠A+∠3=90°,
而OA=OE,
∴∠1=∠A,
∴∠2=∠3,
而∠3=∠4,
∴∠2=∠4,
∴PE=PF.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了垂径定理的推理.

练习册系列答案
相关题目
在Rt△ABC中,∠ACB=90°,CD是AB边上的高,则下列结论:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④CD•AD=AC•BC;⑤
=
,正确的个数有( )
| AC2 |
| BC2 |
| AD |
| BD |
| A、2个 | B、3个 | C、4个 | D、5个 |
一直角三角形的斜边长比一直角边长大2,另一直角边长为6,则斜边长为( )
| A、4 | B、8 | C、10 | D、12 |
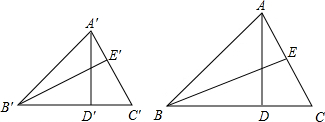 如图,AD、BE是△ABC的两条高,A′D′、B′E′是△A′B′C′的两条高,△ABD∽△A′B′D′,∠C=∠C′,求证:
如图,AD、BE是△ABC的两条高,A′D′、B′E′是△A′B′C′的两条高,△ABD∽△A′B′D′,∠C=∠C′,求证: 如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由.
如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由.