题目内容
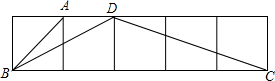如图所示，点A、B、C、D在正方形网格的格点上，求∠BDC的度数．考点：相似三角形的判定与性质
专题：网格型
分析：首先求出△BDC，△ABD的三边长（用字母λ表示），进而证明△BDC∽△DAB，得到∠BDC=∠BAD，问题即可解决．
解答：解：设每个正方形网格的边长为λ，
由勾股定理得：
AB2=2λ2，BD2=4λ2+λ2，DC2=9λ2+λ2，
∴AB=
λ，BD=
λ，DC=
λ，而BC=5，
∴
=
=
=
，
∴△BDC∽△DAB，
∴∠BDC=∠BAD，
而∠BAD=180°-45°=135°，
∴∠BDC=135°．
解：设每个正方形网格的边长为λ，由勾股定理得：
AB2=2λ2，BD2=4λ2+λ2，DC2=9λ2+λ2，
∴AB=
| 2 |
| 5 |
| 10 |
∴
| DC |
| AB |
| BC |
| BD |
| BD |
| AD |
| 5 |
∴△BDC∽△DAB，
∴∠BDC=∠BAD，
而∠BAD=180°-45°=135°，
∴∠BDC=135°．
点评：该题主要考查了相似三角形的判定及其性质定理的应用问题；解题的关键是准确判断、灵活推理、科学论证．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
下列四个图形中，是轴对称图形，且对称轴只有一条的图形是（ ）
A、 |
B、 |
C、 |
D、 |
在下面实数中，无理数是（ ）
A、-
| ||
B、
| ||
| C、2 | ||
| D、3.14 |
某产品进货单价为90元，按100元一件出售时，能售出500件．若每件涨价1元，则销售量就减少10件．则该产品能获得的最大利润为（ ）
| A、5000元 |
| B、8000元 |
| C、9000元 |
| D、10000元 |
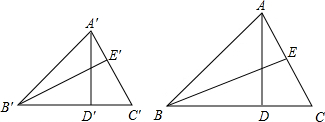如图，AD、BE是△ABC的两条高，A′D′、B′E′是△A′B′C′的两条高，△ABD∽△A′B′D′，∠C=∠C′，求证：
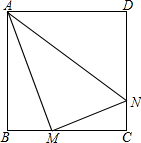如图，正方形ABCD边长为4cm，M、N分别为BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．