题目内容
5. 在Rt△ABC中,若∠C=90°,cosB=$\frac{1}{3}$,AC=5,求AB的长.
在Rt△ABC中,若∠C=90°,cosB=$\frac{1}{3}$,AC=5,求AB的长.
分析 根据题意设BC=x,AB=3x,利用勾股定理可得方程x2+52=(3x)2,解方程可得x的值,进而可得AB的长.
解答 解:∵∠C=90°,cosB=$\frac{1}{3}$,
∴设BC=x,AB=3x,
∵AC=5,
∴x2+52=(3x)2,
解得:x=$\frac{5\sqrt{2}}{4}$,
∴AB=$\frac{15\sqrt{2}}{4}$.
点评 此题主要考查了解直角三角形,关键是掌握余弦定义,掌握勾股定理:两直角边的平方和等于斜边的平方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知某种儿童米粉的标准质量为200g,苏果超市从购进的儿童米粉中随机抽取8袋检测每袋的质量是否符合标准质量,超过与不足的质量分别用正、负数表示,例如+2表示该袋米粉超过标准质量2g,现记录如表:
(1)指出编号为几的米粉最接近标准质量?
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 偏差 | +1 | -2 | -1 | -2 | -0.5 | +4 | +2 | -1 |
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?
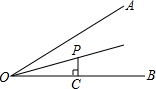 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.

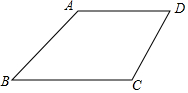 如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD=$\frac{4}{3}\sqrt{6}$,BC=4$\sqrt{2}$,求CD的长.
如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD=$\frac{4}{3}\sqrt{6}$,BC=4$\sqrt{2}$,求CD的长. 如图,在△ABC中,AB=3,AC=5,AD是中线,点E在AD的延长线上,且AD=ED=2,求△ABC的面积.
如图,在△ABC中,AB=3,AC=5,AD是中线,点E在AD的延长线上,且AD=ED=2,求△ABC的面积.