题目内容
14.解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{2}+\frac{1-x}{3}>1}\\{5x+1≥3(x+1)}\end{array}\right.$,并在数轴上把它的解集表示出来.分析 分别解两个不等式得到x>$\frac{7}{4}$和x≥1,然后根据大大取大确定不等式组的解集,最后用数轴表示解集.
解答 解:$\left\{\begin{array}{l}{\frac{2x-1}{2}+\frac{1-x}{3}>1①}\\{5x+1≥3(x+1)②}\end{array}\right.$,
由①得:x>$\frac{7}{4}$,
由②得:x≥1,
所以这个不等式的解集是x>$\frac{7}{4}$,
用数轴表示为:
点评 本题考查不等式组解集的表示方法和一元一次不等式的解法.把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.下列说法正确的是( )
| A. | |-3|=-3 | B. | 0的倒数是0 | C. | 9的平方根是3 | D. | -4的相反数是4 |
8.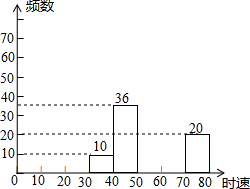 为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.
为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.
注:30-40为时速大于等于30千米,而小于40千米,其他雷同.
(1)监测到的这一组汽车的总数是200辆;
(2)请你把表中的数据填写完整,并补全频数分布直方图;
(3)若依据图表作扇形统计图,数据段“70~80”所对应的圆心角是36度;
(4)如果汽车时速不低于60千米/时即为违章,则监测到的违章车辆共有多少.
 为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.
为保证全运会期间交通顺畅,在连接全运村、场馆及客运枢纽的干道上,将设置全运专用车道.同时交通部门对周边街路进行雷达测速区检测,现将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率图表.注:30-40为时速大于等于30千米,而小于40千米,其他雷同.
| 数据段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | 0.18 |
| 50~60 | 78 | 0.39 |
| 60~70 | 56 | 0.28 |
| 70~80 | 20 | 0.10 |
(2)请你把表中的数据填写完整,并补全频数分布直方图;
(3)若依据图表作扇形统计图,数据段“70~80”所对应的圆心角是36度;
(4)如果汽车时速不低于60千米/时即为违章,则监测到的违章车辆共有多少.
 如图,∠F的内错角有∠AEF和∠ADF.
如图,∠F的内错角有∠AEF和∠ADF.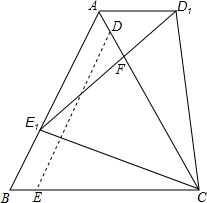 如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$.
如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$. 现在是8点30分,时针与分针所形成的夹角是多少度数?
现在是8点30分,时针与分针所形成的夹角是多少度数?