题目内容
4．n边形的边数每增加一条，其对角线增加（ ）| A． | n条 | B． | （n-1）条 | C． | （n-2）条 | D． | （n-3）条 |
分析 利用n边形对角线的条数为$\frac{n（n-3）}{2}$条，结合实际得出结论．
解答 解：n边形对角线的条数为$\frac{n（n-3）}{2}$条，
边数增加1条后，对角线的条数为$\frac{（n+1）（n-2）}{2}$条，$\frac{（n+1）（n-2）}{2}-\frac{{n}^{2}-3n}{2}$=n-1．
∴n边形的边数增加1条，其对角线增加（n-1）条．
故选：B
点评 本题主要考查多边形的对角线的求法，关键是根据利用n边形对角线的条数为$\frac{n（n-3）}{2}$条分析．
练习册系列答案
相关题目
如图，点P是抛物线y=x2在第一象限内的一个点，点A的坐标是（3，0）．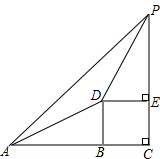
山顶上有一个电视铁塔，从地面A点看铁塔顶P的仰角是45°，沿坡度i=1：$\sqrt{3}$的山坡向 上走了100米，到达D点，再看铁塔顶P的仰角是60°，求铁塔顶P到地面的距离PC（结果保留根号）．