题目内容
15.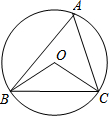 如图,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC+∠BOC=180°,BC=2$\sqrt{3}$cm,则⊙O的半径为2cm.
如图,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC+∠BOC=180°,BC=2$\sqrt{3}$cm,则⊙O的半径为2cm.
分析 如图作OE⊥BC于E.首先证明∠BOC=120°,在Rt△BOE中,易知OB=2OE,设OE=x,OB=2x,利用勾股定理列出方程即可解决问题.
解答 解:如图作OE⊥BC于E.
∵∠BAC+∠BOC=180°,∠BOC=2∠A,
∴∠BOC=120°,∠A=60°,
∵OE⊥BC,
∴BE=EC=$\sqrt{3}$,∠BOE=∠COE=60°,
∴∠OBE=30°,
∴OB=2OE,设OE=x,OB=2x,
∴4x2=x2+($\sqrt{3}$)2,
∴x=1,
∴OB=2cm.
故答案为2.
点评 本题考查三角形的外心与外接圆、圆周角定理.垂径定理、勾股定理、直角三角形30度角性质、等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
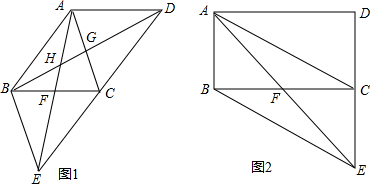
 如图,点B是扇形AOC的弧AC的二等分点,过点B、C分别作半径的垂线段BD、CE,垂足分别为D、E,已知OA⊥OC,半径OC=1,则图中阴影部分的面积和是$\frac{π}{4}$-$\frac{1}{2}$.
如图,点B是扇形AOC的弧AC的二等分点,过点B、C分别作半径的垂线段BD、CE,垂足分别为D、E,已知OA⊥OC,半径OC=1,则图中阴影部分的面积和是$\frac{π}{4}$-$\frac{1}{2}$.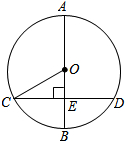 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm.
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm.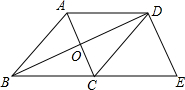 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E. 如图,抛物线y=$\frac{1}{4}$x2+bx+c与两轴交于点A(2,0),点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$,过点A与y轴交于点C,与抛物线的另一个交点是D点.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与两轴交于点A(2,0),点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$,过点A与y轴交于点C,与抛物线的另一个交点是D点.