题目内容
10.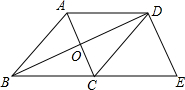 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;
(2)若BD=4,AC=3,求cos∠CDE的值.
分析 (1)想办法证明AC∥DE,AD∥CE即可;
(2)只要证明∠CDE=∠E,再想办法求出cos∠E即可;
解答 (1)证明:∵四边形ABCD是菱形
∴AD∥BC,∠BOC=90°,
∵DE⊥BD,
∴∠BDE=90°,
∴∠BDE=∠BOC,
∴AC∥DE,
∴四边形ACED是平行四边形.
(2)解:∵四边形ACED是平行四边形,
∴AD=CE,
∵AD=BC,
∴BC=CE,
∵∠BDE=90°,
∴DC=CE,
∴∠CDE=∠E
∴cos∠CDE=cos∠E,
∵BD=4,AC=3,∠BDE=90°,
∴BE=5,
∴cos∠E=$\frac{DE}{BE}$=$\frac{3}{5}$,
∴cos∠CDE=cos∠E=$\frac{3}{5}$.
点评 本题考查菱形的性质、平行四边形的判定和性质、解直角三角形、锐角三角函数等知识,解题的关键是熟练掌握平行四边形的判定,学会用转化的思想思考问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.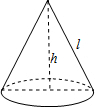 如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
 如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )| A. | 60π | B. | 65π | C. | 78π | D. | 156π |

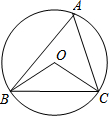 如图,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC+∠BOC=180°,BC=2$\sqrt{3}$cm,则⊙O的半径为2cm.
如图,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC+∠BOC=180°,BC=2$\sqrt{3}$cm,则⊙O的半径为2cm. 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交于矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为8,则k的值为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象交于矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为8,则k的值为( )