题目内容
6. 如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( )
如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
分析 根据三角形中位线定理,可得ED=FG=$\frac{1}{2}$BC=4,GD=EF=$\frac{1}{2}$AO=3,进而求出四边形DEFG的周长.
解答 解:∵BD,CE是△ABC的中线,
∴ED∥BC且ED=$\frac{1}{2}$BC,
∵F是BO的中点,G是CO的中点,
∴FG∥BC且FG=$\frac{1}{2}$BC,
∴ED=FG=$\frac{1}{2}$BC=4,
同理GD=EF=$\frac{1}{2}$AO=3,
∴四边形DEFG的周长为3+4+3+4=14.
故选B.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形中位线的性质定理,为证明线段相等和平行提供了依据.

练习册系列答案
相关题目
17. 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )| A. | 只有①③ | B. | 只有①③④ | C. | 只有②④ | D. | ①②③④ |
16.下列计算正确的是( )
| A. | (a4)2=a6 | B. | a+2a=3a2 | C. | a7÷a2=a5 | D. | a(a2+a+1)=a3+a2 |
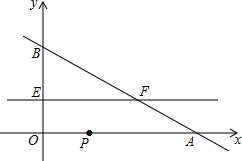 如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题:
如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题: 已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.
已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.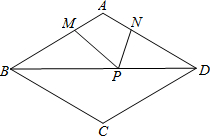 如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.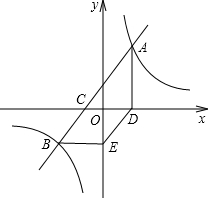 如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.