��Ŀ����
1��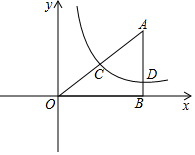 ��ͼ��Rt��ABO��ֱ������ϵ�У�AB��x���ڵ�B��AO=10��sin��AOB=$\frac{3}{5}$��
��ͼ��Rt��ABO��ֱ������ϵ�У�AB��x���ڵ�B��AO=10��sin��AOB=$\frac{3}{5}$����1��������������y=$\frac{k}{x}$��x��0����ͼ��AO���е�C����k��ֵ��
��2���ڣ�1���������£�������������y=$\frac{k}{x}$��x��0����ͼ����AB���ڵ�D������C��Dλ��ֱ��l��y=-x+b�����ʱ����b��ȡֵ��Χ��
��3������D����y��ĶԳƵ�ΪE��������������y=$\frac{k}{x}$��ͼ����߶�AE�й�����ʱ��ֱ��д��k��ȡֵ��Χ��
���� ��1������A��8��6������C��AO���е㣬���C��4��3���������õ�k��ֵ��
��2������õ�C��D�����꣬�ٸ��ݵ�C��Dλ��ֱ��l��y=-x+b����࣬���ɵõ�b��ȡֵ��Χ��
��3���ȸ��ݹ���E�ķ�������������ʽΪy=$\frac{-12}{x}$������A�ķ�������������ʽΪy=$\frac{48}{x}$���ٸ��ݷ���������y=$\frac{k}{x}$��ͼ����߶�AE�й����㣬���ɵõ�k��ȡֵ��Χ��
��� �⣺��1����AO=10��sin��AOB=$\frac{3}{5}$��
��AB=AOsin��AOB=6��OB=8����A��8��6����
�ߵ�C��AO���е㣬
��C��4��3����
�߷���������y=$\frac{k}{x}$��x��0����ͼ��AO���е�C��
��k=4��3=12��
��2����x=8���뷴��������y=$\frac{12}{x}$���ɵ�y=$\frac{3}{2}$��
��D��8��$\frac{3}{2}$����
��D���������ֱ��y=-x+b���ɵ�b=9$\frac{1}{2}$��
��C��4��3������ֱ��y=-x+b���ɵ�b=7��
�ߵ�C��Dλ��ֱ��l��y=-x+b����࣬
��7��b��9$\frac{1}{2}$��
��3���ߵ�D��8��$\frac{3}{2}$������y��ĶԳƵ�ΪE��-8��$\frac{3}{2}$����
�����E�ķ�������������ʽΪy=$\frac{-12}{x}$��
��A��8��6����
�����A�ķ�������������ʽΪy=$\frac{48}{x}$��
�߷���������y=$\frac{k}{x}$��ͼ����߶�AE�й����㣬
��-12��k��0��0��k��48��
���� ������Ҫ�����˷�����������һ�κ����Ľ��������Լ���ֱ�������ε����ã�����ʱע�⣺����������ϵʽ�����ɷ�������⣬���������н��������н��㣬�������⣬���������㣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | a4•a | B�� | ��a2��2 | C�� | a3+a3 | D�� | a4��a |
| A�� | a��b��c | B�� | a��c��b | C�� | b��c��a | D�� | c��b��a |
| A�� | -5 | B�� | -1 | C�� | 1 | D�� | 5 |
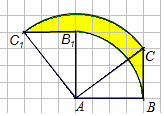 ��ͼ�������������У���ABCΪ��������Σ����㶼�Ǹ�㣩������ABC�Ƶ�A����ʱ�뷽����ת90��õ���AB1C1��������С�����εı߳�Ϊ1cm�����߶�BC��ɨ����ͼ�Σ���Ӱ���֣������Ϊ$\frac{9��}{4}$����������У���
��ͼ�������������У���ABCΪ��������Σ����㶼�Ǹ�㣩������ABC�Ƶ�A����ʱ�뷽����ת90��õ���AB1C1��������С�����εı߳�Ϊ1cm�����߶�BC��ɨ����ͼ�Σ���Ӱ���֣������Ϊ$\frac{9��}{4}$����������У���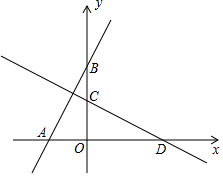 ��ͼ����ƽ��ֱ������ϵxOy�У�����A��-2��0����ֱ�߽�y���������ڵ�B����ֱ��AB���ŵ�O˳ʱ����ת90��ֱ���x�ᡢy�ύ�ڵ�D��C��
��ͼ����ƽ��ֱ������ϵxOy�У�����A��-2��0����ֱ�߽�y���������ڵ�B����ֱ��AB���ŵ�O˳ʱ����ת90��ֱ���x�ᡢy�ύ�ڵ�D��C��