题目内容
18．已知实数n满足等式m=$\sqrt{9+18n}$．（1）当m=6时，求n的值；
（2）若m，n都是正整数，求n的最小值．
分析 （1）根据题意得出9+18n=36，进而解答即可；
（2）根据二次根式的定义进行分析解答即可．
解答 解：（1）因为等式m=$\sqrt{9+18n}$，m=6，
可得：9+18n=36，
解得：n=1.5；
（2）因为实数n满足等式m=$\sqrt{9+18n}$，m，n都是正整数，
可得：9+18n=81，
解得：n=4．
点评 此题考查二次根式问题，关键是根据二次根式的定义进行分析．
练习册系列答案
相关题目
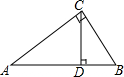在直角三角形ABC中，∠ACB=90°，∠A、∠B、∠C的对边分别是a、b、c，CD⊥AB于点D，若AC=8，BC=6，求AB、AD、BD的长以及三角形ABC的面积．
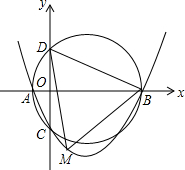如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C的圆与y轴的另一个交点为D．已知点A，B，C的坐标分别为（-2，0），（8，0），（0，-4）．
13．纳米（nm）是非常小的长度单位，已知1nm=10-6mm，某种病毒的直径是100nm，若将这种病毒排成1mm长，则病毒的个数是（ ）
| A． | 102个 | B． | 104个 | C． | 106个 | D． | 108个 |
如图，正方形网格中的每一个小正方形边长都为1，每个小正方形的顶点叫格点，按下面的要求画出以格点为顶点的三角形，并写出它的面积．
如图，在△ABC中，D是BC边上的点，AD=DC，∠BAD=40°，∠C=35°，求证：△ABD是等腰三角形．
一个正方体的每个面都写有一个汉字，其平面展开图如图所示，则在该正方体中，和“我”相对面上所写的汉字是（ ）
8．若凸n边形的内角和为1260°，则从一个顶点出发引的对角线条数是（ ）
| A． | 6 | B． | 8 | C． | 18 | D． | 27 |