题目内容
20.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
分析 (1)利用勾股定理直接计算即可;
(2)设a=3x,c=5x,由勾股定理可求出x的值,进而可求出求△ABC的面积.
解答  解:
解:
(1)∵△ABC中,∠C=90°,b=2,c=3,
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{5}$;
(2)∵a:c=3:5,
∴设a=3x,c=5x,
∵b=16,
∴9x2+162=25x2,
解得:x=4,
∴a=12,
∴△ABC的面积=$\frac{1}{2}$×12×16=96.
点评 此题主要考查学生对勾股定理的理解及运用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.熟记勾股定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.$\sqrt{0.0001}$的算术平方根是( )
| A. | 0.1 | B. | 0.01 | C. | ±0.1 | D. | ±0.01 |
8. 如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB度数为( )
如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB度数为( )
 如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB度数为( )
如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB度数为( )| A. | 70° | B. | 55° | C. | 40° | D. | 35° |
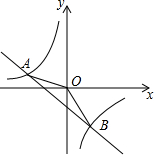 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,2)、B(n,-4)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,2)、B(n,-4)两点.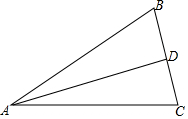 已知:如图,在△ABC中,AD平分∠BAC.
已知:如图,在△ABC中,AD平分∠BAC.