题目内容
4.已知一元二次方程x2-4x+k+1=0有两个不相等的实数根.(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k+1=0与x2+mx+m-1=0有一个相同的根,求此时m的值.
分析 (1)由题意得△>0,得到关于k的不等式,解得即可;
(2)k符合条件的最大整数为2,代入方程x2-4x+k+1=0,解得方程的根,把方程的根分别代入x2+mx+m-1=0即可得解.
解答 解:(1)∵一元二次方程x2-4x+k+1=0有两个不相等的实数根,
∴△=16-4(k+1)>0解得:k<3;
(2)∵k符合条件的最大整数为2,
∴把k=2代入x2-4x+k+1=0得x2-4x+3=0,
解得;x1=1,x2=3,
把x1=1代入x2+mx+m-1=0,得m=0,
把x2=3代入x2+mx+m-1=0,得m=-2,
综上所述,m=0或m=-2.
点评 本题考查了一元二次方程的解法,根的判别式,根的定义,熟练掌握一元二次方程的解法是解题的关键.

练习册系列答案
相关题目
14.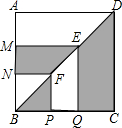 如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
 如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )
如图,正方形ABCD的边长为x,点E、F分别是对角线BD上的两点,过点E、F作AD、AB的平行线,则图中阴影部分的面积的和为( )| A. | $\frac{1}{4}$x2 | B. | $\frac{1}{2}$x2 | C. | $\frac{1}{5}$x2 | D. | $\frac{1}{3}$x2 |
15.下面方程变形中,正确的是( )
| A. | 2x-1=x+5移项得2x+x=5+1 | B. | $\frac{x}{2}$+$\frac{x}{3}$=1去分母得3x+2x=1 | ||
| C. | (x+2)-2(x-1)=0去括号得x+2-2x+2=0 | D. | -4x=2系数化为“1”得x=-2 |
13.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{a+{b}^{2}}$ | B. | $\sqrt{8x}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
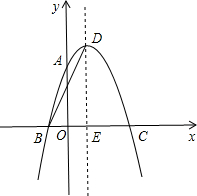 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题: 如图,在每个小正方形边长都为1的正方形网格中,经过格点A、B、C的弧所在圆的面积为$\frac{37}{2}π$.(结果保留准确值)
如图,在每个小正方形边长都为1的正方形网格中,经过格点A、B、C的弧所在圆的面积为$\frac{37}{2}π$.(结果保留准确值) 如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.
如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.