题目内容
9.已知一次函数y=x+b的图象与x轴,y轴交于点A、B.(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=2;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值.
分析 (1)先根据平移的规律求出y=x+b的图象沿x轴向右平移2个单位后的解析式,再将原点的坐标代入即可求解;
(2)先求出y2=kx+4图象与y轴交点,则此交点在函数y=x+b图象上,求出b=4.再求出y1=x+4与x轴的交点坐标为(-4,0),则y2=kx+4的图象经过点(4,0),即可求出k=-1.
解答 解:(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x-2+b,
由题意,得0=0-2+b,
解得b=2.
故答案为2;
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
∵(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(-4,0).
∵y2=kx+4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx+4的图象经过点(4,0),则0=4k+4,
∴k=-1.
点评 本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,关于y轴对称的点的坐标特征,掌握解析式“左加右减,上加下减”的平移规律是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.若x2-2(k-1)x+4是完全平方式,则k的值为( )
| A. | ±1 | B. | ±3 | C. | 1或-3 | D. | -1或3 |

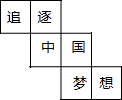 一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )
一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )