题目内容
18.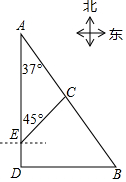 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 如图作CH⊥AD于H.设CH=xkm,在Rt△ACH中,可得AH=$\frac{CH}{tan37°}$=$\frac{x}{tan37°}$,在Rt△CEH中,可得CH=EH=x,由CH∥BD,推出$\frac{AH}{HD}$=$\frac{AC}{CB}$,由AC=CB,推出AH=HD,可得$\frac{x}{tan37°}$=x+5,求出x即可解决问题.
解答 解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°=$\frac{CH}{AH}$,
∴AH=$\frac{CH}{tan37°}$=$\frac{x}{tan37°}$,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴$\frac{AH}{HD}$=$\frac{AC}{CB}$,
∵AC=CB,
∴AH=HD,
∴$\frac{x}{tan37°}$=x+5,
∴x=$\frac{5•tan37°}{1-tan37°}$≈15,
∴AE=AH+HE=$\frac{15}{tan37°}$+15≈35km,
∴E处距离港口A有35km.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
6.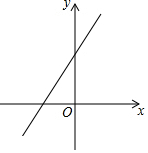 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
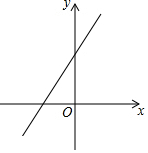 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
3. 如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )
如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )
 如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )
如图示直线l1,l2△ABC被直线l3所截,且l1∥l2,则α=( )| A. | 41° | B. | 49° | C. | 51° | D. | 59° |
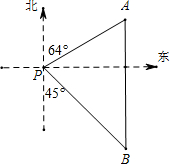 如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).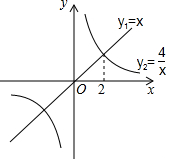 函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.
函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.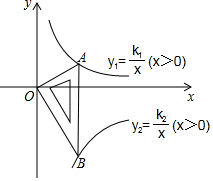 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.
如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.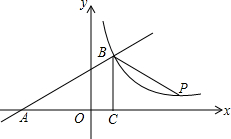 如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.
如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.