题目内容
5．抛物线y=mx2+x-2的最大值是2，则m值为-$\frac{1}{16}$．分析 当抛物线开口向下时，在顶点处取到最大值，只需运用顶点坐标公式就可解决问题．
解答 解：由题可得，
m＜0，且$\frac{4m•（-2）-{1}^{2}}{4m}$=2，
解得：m=-$\frac{1}{16}$．
故答案为-$\frac{1}{16}$．
点评 本题主要考查了二次函数的最值和顶点坐标公式，其中抛物线y=ax2+bx+c（a≠0）的顶点坐标为（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），应熟练掌握．
练习册系列答案
相关题目
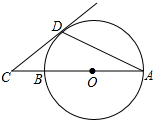如图所示，AB是⊙O的直径，AD是弦，∠DAB=20°，延长AB到点C，使得∠ACD=