题目内容
14.在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字为m,点P的横坐标为(m,m2+1),则点P落在抛物线y=-4x2+8x+5与x轴所围成的区域内(含边界)的概率是$\frac{3}{5}$.分析 画出抛物线图象,确定各点横坐标所对应的纵坐标,与P点纵坐标比较即可.
解答  解:如图,
解:如图,
当m=-2,-1,0,1,2时,m2+1=5,2,1,2,5,
则点P的坐标为(-2,5),(-1,2),(0,1),(1,2),(2,5);
描出各点:-2<-0.5,-1<-0.5,不合题意;
把x=0代入解析式得:y1=5,1<5,故(0,1)在该区域内;
把x=1代入解析式得:y2=9,2<9,故(1,2)在该区域内;
把x=2代入解析式得:y3=5,5=5,故(2,4)在边界上,在该区域内.
所以5个点中有3个符合题意,
点P落在抛物线y=-4x2+8x+5与x轴所围成的区域内(含边界)的概率是$\frac{3}{5}$.
故答案为$\frac{3}{5}$.
点评 此题考查了几何概率,二次函数的图象与性质,综合性很强,不仅要求学生掌握概率公式,更要求学生熟悉二次函数的图象及性质.利用数形结合是解题的关键.

练习册系列答案
相关题目
7. 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )| A. | a+c | B. | c-a | C. | -c-a | D. | a+2b-c |
8.一个长方形的周长为6a-4b,若它的宽为a-b,则它的长为( )
| A. | 5a-3b | B. | 2a-3b | C. | 2a-b | D. | 4a-2b |
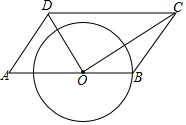 如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.
如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.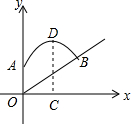 一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.
一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.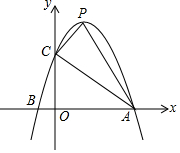 已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.
已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.