题目内容
3.操作发现(1)如图1,已知△ABC,边BC绕点B旋转至BC′位置,试在图中画出△ABC以同样方式旋转得到的图形△A′BC′.
(2)如图2,在△ABC中,AB=6,AC=4.分别以AB、AC为边向外作△ABD和△ACE,使∠BAD=∠CAE,AD=8,AE=3.连接BE、CD,判断BE与CD有什么数量关系?并说明理由.
(3)如图3,某单位拟扩建花坛,已经测得花坛固定部分△ABD中∠A=45°,AD=6$\sqrt{2}$,AB=7.花坛扩建部分△DBC必须保持DB=DC,那么当扩建后花坛四边形ABCD面积最大时,A、C两点之间的距离为多少?
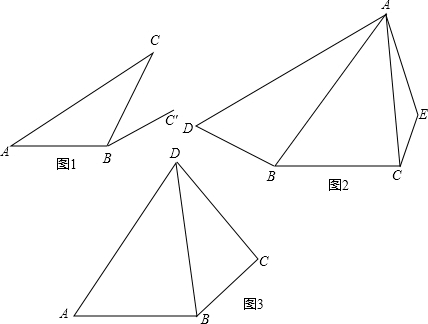
分析 (1)作∠ABA′=∠CBC′,然后截取A′B=AB,C′B=CB,连接A′B,A′C′,C′B,△A′BC′即为所求;
(2)根据相似三角形的判定和性质定理即可得到结论;
(3)过D点作DE垂直于AD,交AB延长线于E点,连接CE,如图,则△DAE和△DBC为等腰直角三角形,根据其性质,可得△ABD≌△ECD,进而得到CE是高,且CE=AB,最后根据勾股定理求出即可.
解答 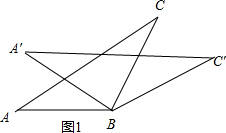 解:(1)如图所示,△A′BC′即为所求;
解:(1)如图所示,△A′BC′即为所求;
(2)连接DC,BE,
∵∠BAD=∠CAE,
∴∠DAC=∠EAB,
∵AB=6,AC=4,AD=8,AE=3
∴$\frac{AD}{AB}=\frac{8}{6}=\frac{4}{3}$,$\frac{AC}{AE}$=$\frac{4}{3}$,
∴$\frac{AD}{AB}=\frac{AC}{AE}$,
∴△ADC∽△ABE,
∴$\frac{DC}{BE}=\frac{AC}{AE}=\frac{4}{3}$;
(3)要使扩建后花坛四边形ABCD面积最大,
∵△ABD为固定部分,
∴△BCD的面积最大,
∴当BD⊥CD时,△BCD的面积最大,
∵BD=CD,
∴△BCD为等腰直角三角形,
如图3,过D点作DE垂直于AD,交AB延长线于E点,连接CE,AC,
则△DAE为等腰直角三角形
∴∠2=45°,
∵BD⊥CD,∠DAB=∠DBC=45°,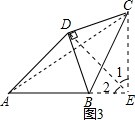
在△ABD和△ECD中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ECD,
∴∠1=∠DAB=45°,
∴∠CEB=90°,
∴CE是高,且CE=AB=7,
∴AE=$\sqrt{2}$AD=12,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{193}$.
点评 本题主要考查了旋转的性质,基本作图,相似三角形的判定和性质,等腰直角三角形的性质和全等三角形的判定与性质,作辅助线,构建等腰直角三角形,是解答本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 2,6 | B. | 12,16 | C. | 16,20 | D. | 20,24 |
| A. | x≥1 | B. | x≠1 | C. | x>1 | D. | x≤1 |
| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | $\frac{24}{5}$ |
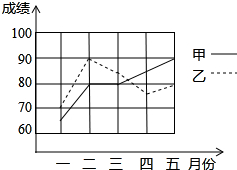 为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数)
为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数) 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.