题目内容
10. 如图,某校数学兴趣小组利用自制的直角三角形小硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为11.5米.
如图,某校数学兴趣小组利用自制的直角三角形小硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为11.5米.
分析 根据题意证出△DEF∽△DCA,进而利用相似三角形的性质得出AC的长,即可得出答案.
解答 解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则$\frac{DE}{DC}=\frac{EF}{AC}$,即$\frac{0.5}{20}=\frac{0.25}{AC}$,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
即旗杆的高度为11.5m;
故答案为:11.5.
点评 此题主要考查了相似三角形的应用;由三角形相似得出对应边成比例是解题关键.

练习册系列答案
相关题目
20.根据下列表格对应值:
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
| x | -1 | 0 | 1 | 1.1 | 1.2 | 1.3 |
| ax2+bx+c | -26 | -15 | -2 | -0.59 | 0.84 | 2.29 |
| A. | x<-1 | B. | -1<x<1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
5.若关于的x方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | -4 | B. | -2 | C. | 2 | D. | -4 |
2.用四舍五入法对0.02015(精确到千分位)取近似数是( )
| A. | 0.02 | B. | 0.020 | C. | 0.0201 | D. | 0.0202 |
19.已知a-b=1,则代数式2a-2b-3的值是( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
20.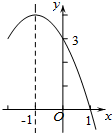 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
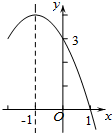 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-3 | D. | x1=1,x2=-4 |