题目内容
9.若x=-2是关于x的一元二次方程x2+$\frac{3}{2}$ax-a2=0的一个根,则a的值为( )| A. | 1或-4 | B. | -1或-4 | C. | -1或4 | D. | 1或4 |
分析 把x=-2代入已知方程,列出关于a的新方程,通过解新方程可以求得a的值.
解答 解:∵x=-2是关于x的一元二次方程x2+$\frac{3}{2}$ax-a2=0的一个根,
∴(-2)2+$\frac{3}{2}$a×(-2)-a2=0,即a2+3a-4=0,
整理,得(a+4)(a-1)=0,
解得 a1=-4,a2=1.
即a的值是1或-4.
故选A.
点评 本题考查了一元二次方程的解的定义.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
14.下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
| A. | a=1.5,b=3,c=3 | B. | a=7,b=24,c=25 | C. | a=6,b=8,c=10 | D. | a=3,b=4,c=5 |
15. 如图,这个棱柱的左视图是( )
如图,这个棱柱的左视图是( )
 如图,这个棱柱的左视图是( )
如图,这个棱柱的左视图是( )| A. |  | B. |  | C. |  | D. |  |
16.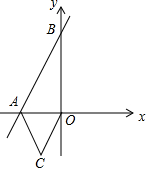 如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )
如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )
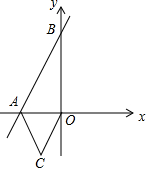 如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )
如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 4-$\sqrt{3}$ | D. | 4$+\sqrt{3}$ |
 关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为x≤2.
关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为x≤2.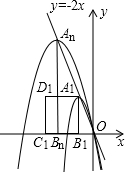 我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线: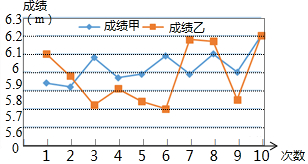 如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)
如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)