题目内容
3.如果点(-2,m)和($\frac{1}{2}$,n)都在直线y=$\frac{4}{3}$x+4上,则m,n的大小关系是:m<n.分析 直接把点(-2,m)和($\frac{1}{2}$,n)代入直线y=$\frac{4}{3}$x+4,求出m与n的值,并比较出其大小即可.
解答 解:因为点(-2,m)和($\frac{1}{2}$,n)都在直线y=$\frac{4}{3}$x+4上,
所以m=$\frac{4}{3}×(-2)+4=\frac{4}{3}$,n=$\frac{4}{3}×\frac{1}{2}+4=4\frac{2}{3}$,
所以m<n,
故答案为:m<n.
点评 本题考查的是一次函数图象上点的坐标特点,.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
13.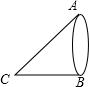 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )| A. | 30米 | B. | 40米 | C. | 50米 | D. | 60米 |
13. 如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )| A. | (6,1) | B. | (0,1) | C. | (0,-3) | D. | (6,-3) |
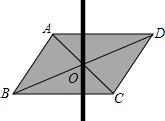 用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条
用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条