题目内容
13.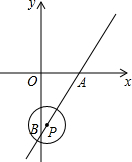 已知如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
已知如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.
分析 (1)由直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,可求得点A与点B的坐标,继而求得∠OBA=30°,然后过点O作OH⊥AB于点H,利用三角函数可求得OH的长,继而求得答案;
(2)当⊙P过点B时,点P在y轴右侧时,易得⊙P被y轴所截的劣弧所对的圆心角为:180°-30°-30°=120°,则可求得弧长;同理可求得当⊙P过点B时,点P在y轴左侧时,⊙P被y轴所截得的劣弧的长;
(3)首先求得当⊙P与x轴相切时,且位于x轴下方时,点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
解答 解:(1)原点O在⊙P外.
理由:∵直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,
∴点A(2,0),点B(0,-2$\sqrt{3}$),
在Rt△OAB中,tan∠OBA=$\frac{OA}{OB}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠OBA=30°,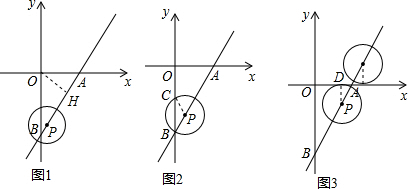 如图1,过点O作OH⊥AB于点H,
如图1,过点O作OH⊥AB于点H,
在Rt△OBH中,OH=OB•sin∠OBA=$\sqrt{3}$,
∵$\sqrt{3}$>1,
∴原点O在⊙P外;
(2)如图2,当⊙P过点B时,点P在y轴右侧时,
∵PB=PC,
∴∠PCB=∠OBA=30°,
∴⊙P被y轴所截的劣弧所对的圆心角为:180°-30°-30°=120°,
∴弧长为:$\frac{120°×π×1}{180}$=$\frac{2π}{3}$;
同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为:$\frac{2π}{3}$;
∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为:$\frac{2π}{3}$;
(3)如图3,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,
在PD⊥x轴,
∴PD∥y轴,
∴∠APD=∠ABO=30°,
∴在Rt△DAP中,AD=DP•tan∠DPA=1×tan30°=$\frac{\sqrt{3}}{3}$,
∴OD=OA-AD=2-$\frac{\sqrt{3}}{3}$,
∴此时点D的坐标为:(2-$\frac{\sqrt{3}}{3}$,0);
当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为:(2+$\frac{\sqrt{3}}{3}$,0);
综上可得:当⊙P与x轴相切时,切点的坐标为:(2-$\frac{\sqrt{3}}{3}$,0)或(2+$\frac{\sqrt{3}}{3}$,0).
点评 此题属于一次函数的综合题,考查了直线上点的坐标的性质、切线的性质、弧长公式以及三角函数等知识.注意准确作出辅助线,注意分类讨论思想的应用.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| 销售量p(件) | P=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=20+x 当20<x≤30时,q=40 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| A. | x≤2 | B. | x≥2 | C. | x>2 | D. | x<2 |
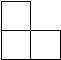 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
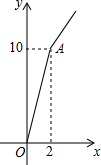 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:| 付款金额 | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
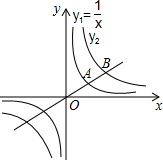 如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$. 如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于130°.
如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于130°.